References on Quantum Electrodynamics
Toichiro Kinoshita, one of my colleagues here at Cornell, is leading the effort in doing careful high-order calculations in quantum electrodynamics. I've drawn my information from two papers of his: The Fine Structure Constant, Rep. Prog. Phys. 59, pp. 1459 (1996), and ``Massively Parallel Computation and the Anomalous Magnetic Moment of the Electron'', to be published.
The latest measurements of g-2 were done by B. Odom, D. Hanneke, B. D'Urso, and G. Gabrielse, Phys. Rev. Lett. 97, 030801 (2006). The latest theoretical calculation is G. Gabrielse, D. Hanneke, T. Kinoshita, M. Nio, and B. Odom, Phys. Rev. Lett. 97, 030802 (2006). A review of the history of this measurement can be found in A. Rich and J. C. Wesley, Reviews of Modern Physics 44 pp. 250 (1972), and in T. Kinoshita, Shelter Island II edited by R. Jackiw, N. N. Khuri, S. Weinberg, and E. Witten (Cambridge, MA: MIT Press) pp. 278-97 (1985).
The quantum Hall measurements of
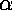were done by
A. Jeffrey et al., 1996 Conference on Precision
Electromagnetic Measurements (17-20 June, 1996, Braunschweig, Germany).
The AC Josephson measurements of
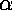were done by
E. R. Williams et al., 1989 IEEE Trans. Instrum. Meas.
38, pp. 233.
The neutron mass measurements of
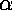were done by
E. Krueger, W. Nistler, and W. Weirauch, 1995 Metrologia 32
p. 117.
Freeman J. Dyson, Physical Review
85, 631 (1952), proved that quantum electrodynamics is an
asymptotic expansion in the
fine structure constant
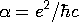; that is, the power series
does not converge
even for 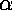as small as 1/137.
Links
- Elastic Theory has Zero Radius of Convergence.
- What is the radius of convergence?
- Famous Asymptotic Series
Last modified: May 24, 1997
James P. Sethna, sethna@lassp.cornell.edu
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).