Water, as it cools to zero Centigrade (32 Farenheit), freezes into ice.
This is a phase transformation: the molecules transform from the
liquid phase into a solid, crystalline phase. At atmospheric pressure,
water will turn to a vapor at 100 Centigrade (212 Farenheit). Both of these
phase transformations are abrupt. H2O is water at 0.0001 C, and
is solid ice at -0.0001 C. (If you add salt or sugar to the water, you can
get slush over a range of temperatures.)
Abrupt phase transitions are called first-order.
The transformation is abrupt as temperature is changed, but it happens
a bit at a time as you add energy. Water and ice coexist at the freezing
temperature. An ice-cube floating in a water glass will keep it at the
freezing point as heat seeps in from the room until it melts. Water when
heated at the boiling point forms bubbles of vapor. The amount of energy
per unit mass it takes to transform water into the new phase is called the
latent heat, L. The ice cube and the
vapor bubble have sharp boundaries separating them from the water, with
a surface tension (or free energy per unit area) s.
It's this surface tension which keeps bubbles and raindrops round.
One can often supercool or superheat at first-order phase transitions. If you put very pure water cold, with no dust particles in it, in a very smooth glass container, it can be supercooled by many degrees DT before freezing into ice. Similarly, water vapor can be supercooled: when it's 110% humidity it means that the water vapor in the air has been supercooled past the temperature at which raindrops can first form.
The reason that you can supercool or superheat through first-order phase
transitions is because there is a free energy barrier separating the two
phases. Simply speaking, you need to make a large bubble of the new
phase in the old one before the new phase can grow. The reason that a
small bubble can't grow is the surface tension s.
Small bubbles pay a large cost in surface tension for a small gain in volume
of the new phase.
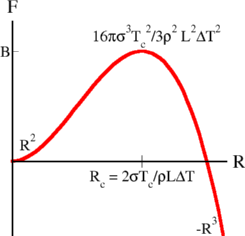
To see this quantitatively, we need a bit of knowledge from statistical mechanics. The free energy of a droplet of radius R is the sum of the energy cost due to the surface tension, 4psR2, and the energy gain due to the volume of the new phase, -(4/3)pR3r Df, where r is the density (mass per unit volume) and the free energy difference per unit mass Df = LDT/Tc. (This follows from the fact that the entropy difference is L/Tc, and that the entropy of each phase is the derivative of the free energy with respect to temperature). Plotting the free energy F(R) (left), we find a radius Rc which gets bigger as the supercooling or superheating DT gets smaller (Rc ~1/DT), and a barrier height that also diverges (B ~1/DT2).
Now, the reason that you can supercool and superheat a container of water is the barrier B. Because you need to nucleate a droplet of the new phase of radius Rc, you need to pay an energy cost B. The nucleation rate is a prefactor times the probability of being on top of the barrier. The probability of being on top of the barrier is given by the traditional Boltzmann (or Arrhenius) factor exp(-B/kT). When the supercooling or superheating gets small, B gets large, and the nucleation rate exp(-B/kT) gets really, really small. It gets so small that, even though the experiment has lots of water and thus lots of places for a new droplet to form, and even though water molecules rearrange very quickly (giving a big prefactor), the probability of nucleating an ice crystal or gas bubble can be negligable.
This is the theory of homogeneous nucleation. Usually in real life the new phase nucleates on some kind of dust particle, or some defect in the material, or some flaw on the surface of the container. (That's why bubbles in soda pop or in boiling water usually form on the sides and bottom of the container, and why people seed clouds to try to get rain.) The atoms in the unstable phase will use any short-cut available, and a dust particle around the size Rc which attracts ice or water can form an easy bypass, allowing the phase transition to occur almost where the equilibrium transition temperature says it should.
James P. Sethna, sethna@lassp.cornell.edu
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).