Explanation

For this simulation data from Briggs (1959)¹ has been used for the large rotational speeds. For the knuckleball (very slow rotational speeds) data from Watts and Sawyer (1975)² has been used. The figure below was made, by using the data from these articles. For more information please refer to the articles.

The simulation

For each time step in this simulation, the acceleration, velocity and distance are calculated by the following equations (until the ball either passes home plate or hits the ground):

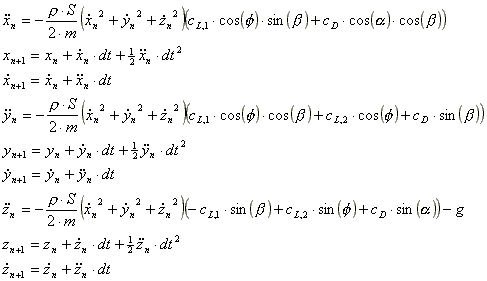
Where:

• is the density of air at sea level                      = 1.225 kg/m³
•  S is the surface area (=, r = 36.576 mm)  = 4.2028×10^-3 m²
• 'm' is the mass of the ball                                   = 0.146 kg
• is the instantaneous angle between the instantaneous velocity and the horizon.
• is the instantaneous angle between the instantaneous velocity in the x-y surface and the x-axes.
• is the constant angle of the baseball around the x-axes.
• C_D is the drag coefficient, which has the same direction as the instantaneous velocity.
• C_L,1 is the lift coefficient, depending on the .
• C_L,2 is the lift coefficient, depending on the rotational speed.
• dt  is the time step ('step size'). After every time step the simulation will be recalculated.
• 'x'  is the coordinate in the direction of the home plate.
• 'y'  is the coordinate perpendicular to the x-axes laying at the field surface.
• 'z'  is the coordinate perpendicular to the field surface in the direction of the sky.

The results will be more accurate using the smallest step sizes, but the simulation will take more time, because of more calculations that has to be made. Here it also serves as a speed control of the animation.

Drag and lift coefficients

The drag coefficient is almost constant for every position and every rotational speed (C_D = 0.5). The C_L,1depends on the orientation of the ball into the air. In figure1 the variation of C_L,1 for different  has been plotted.
At = 0, the separation of the flow will be turbulent on both sides because of the seams. The seams will cause disturbances in the flow and the flow will change from laminar to turbulent. When we turn the baseball a little to > 0, at a certain point on the ball, the flow will not meet any seams anymore at the front of the ball. The laminar flow can't follow the surface of the ball as well and the flow at that point of the flow will separate. The laminar separation will occur much sooner than a turbulent separation. This will cause a much smaller pressure at the side, where laminar separation occurs, which causes a force in that direction. When a larger percentage of the flow at the same side separates laminar, the force will increase.When the position of the ball reaches = 52, 140, 220 or 310o the transition from laminar separation to turbulent separation will occur for in large area at the one side of the ball. At the other side of the ball the opposite will occur. For the angles  = 140 and 220, this causes a discontinuous jump of the force. At the angles q = 52 and 310, an instability will occur that causes the lift coefficient to alternate from left to right with an amplitude of about ±0.18 and a frequency of 0.5-1 cycles/sec. It is more likely that the discontinuous jump at the angles = 140 and 220 will cause the strange trajectory of a knuckleball.

The C_L,2 is linear dependent on the rotational speed. A change in the velocity of the baseball will not change the C_L,2.

The knuckleball

The knuckleball is a slowly pitched ball, which changes its trajectory just before it reaches home plate. It is very difficult for the batter to hit such a pitch. The ball will be pitched almost without rotational speed. When the rotational speed is almost zero the C_L,1 will be the most important lift coefficient. To throw the most effective knuckleball the ball must be thrown with a of around 140 or 220 as a starting angle. The ball must have a very small rotational speed during its flight in the direction, which causes the discontinuous jump. It is not clear if either a couple around the ball will cause the rotational speed or a starting rotational speed has to be thrown. A knuckleball will be pitched at a velocity near 27 m/s.

The curveball

The curveball is a pitch that is thrown with very high rotational speeds. The spinning perpendicular to the ball's velocity will cause a force perpendicular to the spinning and perpendicular to its velocity, which is known as the Magnus effect. The effect explains that spin will delay separation on the retreating side and will enhance it on the advancing side. This will only occur at post-critical Reynolds numbers, when transition from laminar to turbulent has occurred on both sides. This will occur for every pitch.

Literature

1      Briggs, L.J. 1959. Effect of spin and speed on the lateral deflection of a baseball; and the Magnus effect for smooth spheres. Am. J. Phys. 27: 589-96
2      Watts, R.G., Sawyer, E. 1975. Aerodynamics of a knuckleball. Am. J. Phys. 43: 960-63

(Menko Wisse supervised by H. Higuchi)