Vortex Bound States

Quasiparticle Bound States at a Superconducting Vortex Line: Harald Hess's Zero--Bias Tunneling Peak. (Shore, Huang, Dorsey; 41)

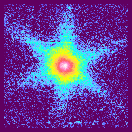
Here is Harald's picture of a vortex line in NbSe_2. Superconductors have a ``gap'' in energy where there are no states (so electrons cannot tunnel in); at a vortex line, the magnetic field closes the gap and there are states to tunnel into. This picture shows the tunneling conductance in the middle of the energy gap, as a function of position on the surface. The six arms are due to the hexagonal crystal structure of the material.

In this picture, the bottom curve is the tunneling conductance far from any magnetic vortex. Notice the gap: the bulges to either side are electron states ``pushed out'' of the gap, and are described by BCS theory. The top curve is the tunneling conductance measured right in the middle of the vortex. There is a peak in the middle, and two valleys on either side. The weird thing Harald discovered was that the gap wasn't just filled in uniformly where the magnetic field came in: the new states were concentrated right in the middle in the big peak. The middle curve is Harald's original measurement at an intermediate distance: more on this in a moment...

Joel Shore, Ming Huang and Alan Dorsey proved my initial ideas wrong, but we predicted that if Harald measured the density at a point off--center he should see a split peak: the electron states don't concentrate in the middle of the energy gap if you aren't in the middle of the vortex.

When Harald lowered the temperature, that's just what he saw. The picture on the left is our theory: if you go out to around the edge of the vortex (one ``coherence length'' away from the center) we predicted that the central peak should split in two. In Harald's experiment, on the right, the front-most curve is measured 800 Å away from the center of the vortex. and you can see the central peak splits as you move from the center outward.

References

H. F. Hess, R. B. Robinson, R. C. Dynes, J. M. Valles Jr., J. V. Waszczak, Phys. Rev. Lett. 62, 1691 (1989).

Joel D. Shore, Ming Huang, Alan T. Dorsey, and James P. Sethna, Phys. Rev. Lett. 62, 3089 (1989).

Harald Hess's Web Page

Links Back

Sethna's Research 90-94

Entertaining Science done at

LASSP.

Statistical Mechanics: Entropy, Order Parameters, and Complexity, now available at Oxford University Press (USA, Europe).