Equilibrium Crystal Shapes
|
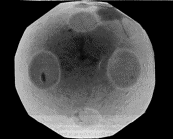
An equilibrium crystal simulated by
Gerard Barkema
and Mark Holzer, here at Cornell (unpublished).
|
A perfect crystal, sitting in a large container, in perfect equilibrium,
will have a shape which is determined by the different energies needed to
make a crystal/vapor boundary in different directions with respect to
the crystalline lattice. The faces aligned along certain crystalline
directions have lower energy, and so one gets faceted crystal shapes
(crystals with flat walls along low-energy directions) at low temperatures.
This is not the reason diamond rings and salt grains have facets! The
salt crystals on your table have facets because they break that way:
diamonds have facets because jewellers grind them with great patience.
It takes careful experiments to see these shapes:
they've been seen in salt (NaCl), gold, lead,
and in the blue phases of chiral nematic liquid
crystals.
|
|
|
|
A salt crystal (NaCl),
at 710 C. The six
faces along the crystal lattice directions are flat, or faceted.
(Heyraud and Métois, J. Cryst. Growth 84,
503 (1987)).
|
A gold crystal at about 1000 C,
(Heyraud and Métois, J. Cryst. Growth 50,
571 (1980); Acta Metal. 28, 1789 (1980)).
|
A lead crystal
at about 300 C.
Prepared by Heyraud and Métois (Rottman et al., Phys. Rev. Lett.
52, 1009 (1984).
|
Rock crystals like quartz aren't
showing equilibrium facets either: they develop facets because of the way
they grow (rather than because it's the shape they like the best).
Around (but below) their melting temperatures, crystals tend to have
shapes which are pretty round: not a complete sphere, but with no
regions which are flat (faceted). This is because at high temperature
the atoms on the surface jiggle and wiggle more: they don't care
so much which places are easier to sit because they have so much
energy to spare. The facets appear at lower temperatures, as the
crystal is cooled: the first temperature at which a facet occurs is
called the roughening temperature. The facets start out
small and close to the special directions; as the temperature
goes down, they become larger.
Heating up to the roughening transition.
(Perversely, it's called the roughening temperature because the
nice, flat face becomes all bumpy and rugged above that temperature.
Of course, the microscopic bumpy, rugged face with the wiggly and jiggly
atoms makes the nice smooth, round shapes you see in the experiments:
the ``rough'' phase has round faces and the ``smooth'' phase has facets.)
|
|
A salt (NaCl) crystal in equilibrium at a cooler
temperature of 620 C.
(Heyraud and Métois, J. Cryst. Growth 84,
503 (1987)).
|
At even lower temperatures, for some crystals, the flat facets begin to
merge, leading to a shape with sharp edges (at the edge rounding temperature).
At lower temperatures still (below the corner rounding transition), the
equilibrium crystal shape is predicted to show sharp corners.
(It's easy to have sharp edges and corners if you cut or cleave the
crystal that way. It's easy to grow crystals with edges and corners.
Think, though, of how weird it would be to sand off the corners of your
diamond ring, wait for a while, and see them re-form by themselves!)
It's been really hard for experimentalists to see these corners. They
tell us that the crystals get really slow and sluggish just around where
the corners would form. Joel Shore studied this problem in our group,
when we were trying to understand why glasses get sluggish just before they
freeze. The way the crystal finds the right shape is a lot like the way
coarsening occurs when a
material (like a metal) with lots of small crystalline regions is annealed to
let the big regions grow at the expense of small ones. Joel
showed that coarsening looks
completely different if the regions have sharp corners!
More Information
Much of the information here is derived from Michael Wortis, in
``Chemistry and Physics of Solid Surfaces VII,'' Springer Series in
Surface Science 10, ed. R. Vanselow and R. Howe, pp. 367 (1988).
Last modified: February 11, 1995
Jim Sethna, sethna@lassp.cornell.edu
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
