Box Counting Method

Package Overview

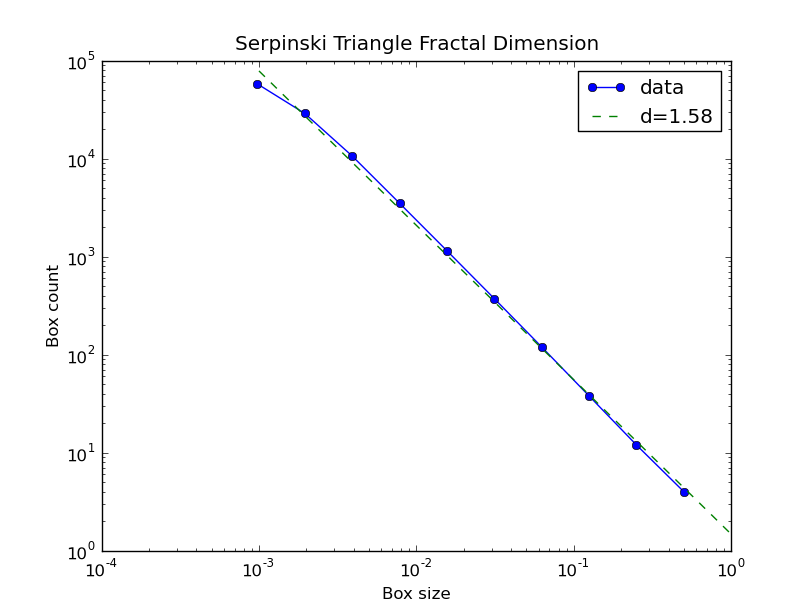
Performs standard box counting techniques to a set of floating point data, first converting the data to binary using a cutoff. For example, it was applied to the Serpinski triangle as an image for the following result:

Module Listing

BoxCountingMethod.BoxCountingMethod(data, cutoff=0.0, periodic_boundary_condition=True)

This method works for fractal structures from 1D to 3D.

If data is not a binary array, it will be converted according to the cutoff. That is, values above cutoff will be counted as 1, below it as 0.

By default, the data array has the same length along all axes, and the length is usually a power of 2. So the boxsizes are given as a list of powers of 2. Certainly, you can supply a special list of boxsizes for any certain system size L.

For example, if data is an array of [128,128], the boxsizes are given by boxsizes = [1,2,4,8,16,32,64].

This function will return two numpy arrays: the former is the array of normalized boxsizes, and the latter is the corresponding array of the total number of ‘black’ boxes.

BoxCountingMethod.Demo()

Shows a simple example of taking random data and using the box-counting method on it with a cutoff of 1/2

BoxCountingMethod.DivideIntoBoxes(data, boxsize)

Does the box counting by taking every boxsized-th element of the array by first adding all of the elements in a box then translating it to a binary value of has data or not.

Binary data should be 1 for occupied sites and 0 for unoccupied.

Along every axis, the length of data array should be divided by the boxsize.

BoxCountingMethod.Run(inputfile, shape, outputfile, cutoff, input=None)

Input array can be provided either as a numpy array to the input argument or as a space separated file given as inputfile. Output is a plot of the number of boxes against the box size.