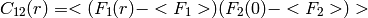Correlation Functions¶
Package Overview¶
This package calculates general spatial correlation functions of scalar, vector, and tensor fields contained in numpy.array like data structures. These data structures can be in the form:
- (dim[0], dim[1], ..., dim[N]) - scalar field in N dimensions
- (M, dim[0], ..., dim[N]) - a length M vector field in N dimensions
- (K, L, dim[0], ..., dim[N]) - a KxL tensor field in N dimensions
To find the correlation function, call one of CorrelationFunctionsOf{Scalar,Vector,Scalar}Field or RadialCorrelationFunctions if you can assume radial symmetry. A radial correlation function can also be produced from a correlation function made from the first set of functions.
For some examples:
1 2 3 4 5 6 7 8 9 10 | import numpy as np
import pylab as pl
import CorrelationFuncions as cf
# create a 3d vector field on a 2d grid
vec = np.random.random((3,128,128))
# calculate the radial correlation
corr = cf.RadialCorrelationFunctions(vec, type='vector')
pl.loglog(corr[0], corr[1], 'o-')
|
Module Listing¶
- CorrelationFunction.BinData_Log(x, y, num_of_bin=50, vmin=None, vmax=None)¶
- Takes log-space histogram of data, dividing x into equally spaced bins in log space and average the y values inside every bin.
- CorrelationFunction.CorrelationFunctionsOfScalarField(field, type='default')¶
- Return the correlation function of variety ‘type’. Can be in:
‘default’: typical autocorrelation function from convolution ‘height-height’: height-height correlation function ‘zero-average’: remove any non-zero offset from all data
then take default autocorrelation
- CorrelationFunction.CorrelationFunctionsOfTensorField(field, type='default', option='total')¶
Return the correlation function of variety ‘type’ for a 3x3 component tensor field, adding all components together. ‘type’ can be one of:
‘default’ : typical autocorrelation function from convolution
‘height-height’: height-height correlation function
- ‘zero-average’ : remove any non-zero offset from all data
then take default autocorrelation
- The argument ‘option’ specifies the symmetry group of the correlation function, being:
- ‘total’ :
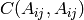
- ‘permutation’ :

- ‘trace’ :
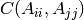
- ‘total’ :
- CorrelationFunction.CorrelationFunctionsOfVectorField(field, type='default')¶
Return the correlation function of variety ‘type’ for a three component vector field, adding all components together. ‘type’ can be one of:
‘default’: typical autocorrelation function from convolution
‘height-height’: height-height correlation function
- ‘zero-average’: remove any non-zero offset from all data
then take default autocorrelation
- CorrelationFunction.RadialCorrFuncFromSpatialCorrFunc(Corr)¶
Averages angle dependence in correlation function assuming spherical symmetry (in the appropriate dimension).
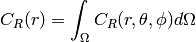
- CorrelationFunction.RadialCorrFuncFromSpatialCorrFuncFast(corr)¶
Averages angle dependence in correlation function assuming spherical symmetry (in the appropriate dimension). This version uses weave to increase speed.
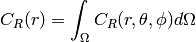
- CorrelationFunction.RadialCorrelationFunctions(field, fieldtype, corrfunctype='default', symmetrytype='total', logbinning=True, binnum=50, fast=True)¶
Calculates the radial correlation function of a field of type fieldtype.
fieldtype can be one of {‘tensor’, ‘vector’, ‘scalar’}
- symmetrytype specifies the symmetries of the tensor field and is one of
{‘total’, ‘permutation’, ‘trace’}
- corrfunctype specifies the variety of correlation function to run:
{‘default’, ‘height-height’, ‘zero-average’}
- CorrelationFunction.Run(inputfile, input, shape, fieldtype, corrfunctype, symmetrytype, logbinning, binnum, outputfile, plot)¶
Performs RadialCorrelationFunctions on an inputfile that holds field data in the space separated values of arbitrary arrangement (i.e. rows / columns don’t matter).
Input is either by filename or by numpy.array. If input is specified it is taken to be the data array. If not, the inputfile is opened and read for data.
- data structure: array.shape should be like (dimension, dimension[0], dimension[1], ...).
- examples:
- one dimensional 3-component vector field with 256 values - (3, 256)
- three dimensional 3-component vector field - (3, 256, 256, 256)
- 3x3 3d tensor field - (3, 3, 256, 256, 256)
- CorrelationFunction.SpatialCorrelationFunction(Field1, Field2)¶
Designed for Periodic Boundary Condition.
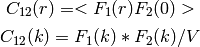
- CorrelationFunction.SpatialCorrelationFunction_HeightHeight(Field1, Field2)¶
Designed for Periodic Boundary Condition.
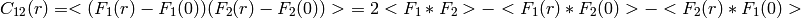
- CorrelationFunction.SpatialCorrelationFunction_ZeroAverage(Field1, Field2)¶
Designed for Periodic Boundary Condition.