Monte Carlo Simulation

The collection of random surfaces that we study to learn about quantum gravity cannot be just any old set of random surfaces. Lets look at an example. Suppose we wanted, for some reason to study the way a handful of marbles end up after they have fallen to the floor. You could actually do the experiment several times and drop a handful of marbles the might see them roll and stop at positions like this:

Now suppose you wanted to study dropped marbles, but had no marbles, or more realistically, you wanted to look at a collection of 100,000 configurations of dropped marbles but did not want to spend weeks dropping marbles and picking them up again. You might write a computer program to generate simulated configurations of dropped marbles. If the most of the simulated marble drops looked somewhat like these below, you might conclude it wasn't a very good simulation. Why?

The second set of configurations seem to have all of the marbles in a line. While it is certainly possible for dropped marbles to line up, we'd expect it to occur only very, very rarely. There are really nearly an infinite number of ways that a handful of marbles could drop to the floor. As its not possible even for the computer to study every way, we'd like the collection of configurations that the computer simulates to be representative of what we'd expect in real life, with the rarer types of configurations showing up less often and the more likely ones occuring more frequently.

The same is true when trying to generate a collection of random surfaces to study to learn about quantum gravity. We want the generated surfaces to be representative of the types if surfaces we expect would be mixed up to make a two dimensional quantum gravity space.

First we say that the simulated surface contains energy. There are many different ways that energy might be stored in a surface. For our surface we will imagine that the energy is stored in two places. First, we will let the links in our simulation all behave as little springs. A spring likes to be as short as possible. It can only be stretched out if someone has put energy into stretching it. In general the farther a spring is stretched, the more energy it is storing. Play with the spring below to see how much energy it stores when it is stretched to different lengths. Use the mouse to drag the block on the end of the spring. The force used to move the block is shown on the left graph (marked F) and the stored energy (marked E) is shown on the right.

Secondly, where two triangles meet along a link, the link behaves like a swinging restaurant door hinge with a spring in it that tries to keep the door shut and flat with the wall. In other words, these springy hinges try to flatten out the surface. When the two triangles along a link are folded together they hold the most energy, and when they are flat the hinge holds the least energy, as shown below.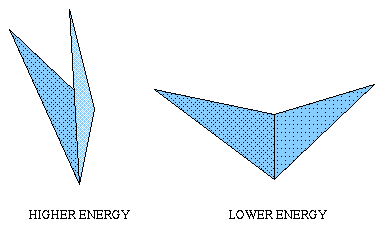

Now, we will have our surface follow the general rule that the more energy it takes to form a triangulation of a particular configuration, the less likely that configuration is to occur. It is this rule, along with how we have allowed the model to store energy that makes the distribution of simulated surfaces representative of the the surfaces that might be found in a "real" two dimensional quantum space-time.

Now lets examine exactly how we can use Monte Carlo simulation methods to have a computer generate collection of independent simulated random surfaces that are representative of two-dimensional quantum gravity.

First the computer generates, from scratch, a random surface without paying any attention to the energy of that surface. This is merely a starting point. Then it picks a link at random and examines what would happen if that link were flipped. If flipping the link would lower the energy of the surface then the link is flipped. If flipping the link would increase the energy of the surface the computer must pick at random whether of not to flip the link. It is more likely that the computer will decide to flip the link if the increase in energy is small. A large increase will make it less likely that the link will be flipped.

Hold the mouse button down over the bold link and see how likely it is that that link would be flipped.

After a number of link flip attempts, the computer picks a node at random. Then it proposes a new position to which the node should be moved. If such a move lowers the energy of the surface then the node is moved to the new position. If the move would increase the energy of the surface then the computer must again decide at random whether to flip the link. And again, if the increase is small the node is more likely to be moved, and if it is a large increase in energy the node is unlikely to be moved.

Use the mouse to drag the central point in this triangulation and see how the energy changes and what the probability is for such a proposed move to be accepted.

After a number of attempted node movements, link flips are attempted again. The process repeats. Each set of link flips and node movements is called a sweep At first, many many sweeps of node movements and link flips must be performed so the current surface no longer looks like the randomly produces starting surface and the surfaces start to be produced in a distribution resembling the quantum gravity distribution. Then the subsequently produced surfaces can be studied.

Watch a two dimensional quantum gravity simulation