 |
Simulating Quantum Gravity
As we described earlier, one might imagine that on a very, very small scale,
space may be a wild blur consisting of a combination of every imaginable kind
of curvature. Physicists can use computer simulations to study
what the small scale structure of space time may be like.
Physicists write computer programs that generate thousands of
simulated surfaces, each with a different random curvature and geometry.
Then they study the collection or ensemble of these surfaces
together.
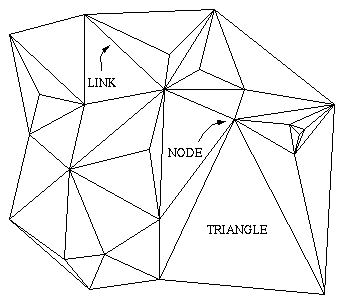One way to simulate a surface is to use a triangulation. Instead of
keeping track of every spot on the surface, we can approximate a two
dimensional surface
with a mesh made of triangles. An example of a triangulation is shown at
left. The points at the corners of the triangles are called nodes.
The lines that join the nodes and form the sides of the triangles
are called links. The triangles themselves are sometimes called
simplexes, and this is why the science of studying quantum gravity
this way is called simplicial quantum gravity.
In the simplest of all simplicial quantum gravity simulations, the
computer must only keep track of how the nodes are connected to form
triangles.
|
To find out more about shapes and curvature, try this
experiment.
You will need some drinking straws and a stapler...
|
In other cases we may also keep track of the position of each of the nodes as
well.
How do we generate the collection of random surfaces? Physicists
need to generate thousands and thousands of different random surfaces
to do a good simplicial quantum gravity simulation. To do this the computer
builds on triangulated surface and then gradually changes its geometry.
It
does this in two ways:
Moving Nodes The computer can grab one of the nodes,
or points on the lattice at random and try to move it a little bit in any
direction.
Flipping Links The computer may pick two triangles that are
next to each other and try to take out the side or link that they
share. Then it replaces it so that it now connects the node on each
triangle that was opposite the old link that they used to share.
|
|
Use the mouse to drag the central point in this triangulation
to a new position.
|
|
|
Click on the bold link in the center to flip it.
|
After enough moving nodes and flipping links the surface looks different
enough from the old one that we consider it an independent
configuration. The computer performs some measurements on this simulated
surface and records this information. Then more link flips and node moves are
performed to generate a new independent random surface. The process is
repeated until enough independent configurations are measured.
|
