Comparison of Exact and Approximate Solutions to the Pendulum
G1: Exact and Approximate Pendulum Equations
The exact equation of motion for the pendulum, as we discussed in the
introduction, is

The term sin(Theta) in this equation makes it hard to solve
analytically. For small angles, 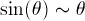 , and the
approximate pendulum equation of motion
, and the
approximate pendulum equation of motion
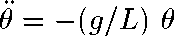
is much easier to solve.
Before starting the analysis, start the pendulum (set to "exact") at several
angles, including as straight up as you can manage, and see qualitatively
how the period and frequency of the motion changes. How large can you make
the period? How small?
(G1a) The Frequency for the Linear Approximation
(G1a.1)
Calculate the frequency in cycles per second for the approximate
pendulum equation of motion, as a function of the mass, g, and L.
Add the formula to your writeup. Evaluate it for the
parameters of our problem (Mass=50 gm, g=9.81 m/s^2,
and L=10 m).
(G1a.2)
Change the menu on the upper left hand corner of galileo
from "exact" to "approx". The pendulum program is now simulating the
approximate pendulum equation of motion. Start at Theta = 0.7, ThetaDot = 0,
(and of course leave the damping alpha=0), and run. Measure the
period for one oscillation, to at least three significant figures.
- Zoom in on the graph with the right mouse button, to get a good measure
of the period. (At large magnifications, you can see the line segments
that the computer uses in its numerical solution to the equation.)
To restore the original size, click with the right mouse button. Hold
the left mouse button down at a point to get the coordinates.
- You will find it easier to get the period from the plot of
ThetaDot vs. Time. Measuring zero-crossings is easier than measuring
the location of a local maximum.
- If you want a more accurate answer, try changing the time step to
a smaller value. Select "Configure", and type in 0.01 for
dt, and then type Return.
This will slow the program down: for those of you with fast machines, that
might be a good thing. Change it back to 0.05 afterward, if you like.
Add the period to your writeup.
(G1a.3)
From the period, compute the frequency given by the simulation.
Compare to the frequency given by the analytic formula, and
include this comparison in your writeup.
Make sure they agree to the accuracy
you expect from the simulation! Does the
frequency change as you increase the initial angle? If
you pick an initial angle greater than pi, you'll see a qualitative difference
between the exact and approximate solutions!
(G1b) Comparing the Frequencies: Exact vs. Approximation
(G1b.1)
Change the menu on the upper left hand corner of galileo from
"approx" to "exact". Galileo is now simulating the exact
pendulum equation of motion. Again, starting at Theta = 0.7, ThetaDot = 0,
measure the period for one oscillation, to at least three significant
figures. The motion should look quite close to a sinusoidal motion, but
with a slightly different frequency from that of the approximate
solution. Write the period in your
writeup. Use the "Copy Graph" button to open a new window and store
the graph there. Using the "configure" button on the new window, label
the curve "Exact" and change the color. (You should probably
use "black", "gray", or "light gray". "Turquoise" will work, but might
print out the same color as "green" on a gray-scale laserprinter.)
(G1b.2)
Change back to "approx", and run from the same initial conditions. Using
the "steal data" button on the new graph window, load the approx curve into
the stored graph. If you already haven't done so, close the configure window
for the graph, and then use the "configure" button again to label the second
curve. Does your name appear on the graph as the title?
Use the "save postscript..." button to store this graph, and
make a printout for your writeup unless your TA tells
you otherwise. (You'll need a PostScript printer, or a translator which
converts for your printer. CIT has PostScript printers available for
a fee per page.)
(G1b.3)
Is the exact period larger or smaller than the approximate one? Is the
exact frequency larger or smaller than the approximate one? In your
writeup, explain this difference. Do so in four ways:
- By expanding sin(theta) to third order in theta, explain how the
difference between the approximate and exact values for ThetaDotDot should
lead to the observed frequency difference.
- By clicking with the left mouse button, start the pendulum at a
value of Theta nearly straight up. (What value of Theta is this?)
How does the period of the approximate motion change? Of the
exact motion? What would happen if you started straight up? In this
extreme case, does the direction of the frequency shift agree with that seen at small
values of the initial Theta?
- Plot (as above) the potential energy vs. theta, for both the
approximate and exact equation of motion, on the same graph. (The
range will be determined by the initial value for Theta: pick it
nearly straight up.) Label the
curves, print the graph, and include in your writeup.
Which potential
energy grows more quickly? What should that do to the frequency?
- Plot the torque vs. theta, for the exact and approximate equation
of motion, and include in your writeup. A larger torque should produce
a more rapid response. Does that help explain the frequency shift?
(G1c) Pendulum Frequency vs. Amplitude
We know that the solution to the approximate equation of motion is a
sinusoid, where the frequency of the sinusoid is independent of the maximum
amplitude of oscillation. However, you might expect that the frequency shift
that you observed in the previous section is a function of the maximum
amplitude of the swing of the pendulum. This is because in the limit
as the initial Theta becomes very small, the approximation
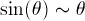 becomes better and better.
becomes better and better.
Set the simulation to "exact". Generate the solution to the exact pendulum
equation of motion for the initial value Theta_0 equal to 0.05, 0.3, 0.9,
1.2, and 1.8, and measure their periods, using the methods noted
above. (You need not make a combined plot for all these curves.)
Using your own program (or graph paper!), make a plot of frequency vs.
initial amplitude and include in your writeup.
The main message of this part of this problem is that the harmonic
approximation sin(theta) ~ theta is an approximation! It works
remarkably well for small displacements, but for larger amplitudes it
breaks down. For the rest of this course, we will be studying wave
equations based on this same linear, harmonic approximation. For most
systems, the wave equation has important corrections if the waves have
large amplitudes --- just like the pendulum. For very large amplitudes,
the differences between the linear theory and the nonlinear theory
can become qualitative, not just quantitative.
(G1d) Qualitative Change
Start with an initial value of Theta of three, and an initial
value for ThetaDot equal to one. What does the motion look like now?
In your writeup, explain how this motion is qualitatively
different from the oscillations around the bottom of the well seen for the rest
of this problem.
Links Back
 Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).


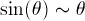 , and the
approximate pendulum equation of motion
, and the
approximate pendulum equation of motion
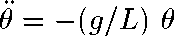
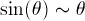 becomes better and better.
becomes better and better.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).