G2: The Damped Pendulum

A problem that is difficult to solve analytically (but quite easy on the computer) is what happens when a damping term is added to the pendulum equations of motion. Here we will use the computer to solve that equation and see if we can understand the solution that it produces.

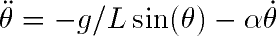
A viscous damping force, modeling for example the viscous damping of the oil in the bearing at the pendulum hinge, would to a good approximation be proportional to the angular velocity of the pendulum, with a coefficient we'll call alpha. The damping force will tend to slow down the pendulum, which determines the sign of the new term in the damped pendulum equation of motion:

(G2a) Playing with the Damping

(G2a.1) Set the damping to 0.1. How much does the amplitude decay in the first two periods? (You'll have to increase the "Time to Run"). For the purposes of this problem, we'll call two periods the point where Theta reaches its maximum (the second full hump of Theta vs Time). Measure (for the next problem) the time at which this occurs.

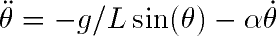
The amplitude for alpha = 0.1 should decay roughly by a factor of two after two periods. Find the value of the damping coefficient alpha needed to make the amplitude decay to precisely half of its value after two periods, and add it to your writeup. Try to measure this alpha to better than two significant figures.

(G2a.2) Take your numerical solution for the first part of this question (with your optimal value for alpha), and make a combined plot of the energy, the potential energy, and the kinetic energy as a function of time, labeling each curve. Save this plot and include it in your lab writeup. In your writeup, address the following questions:

Is the total energy the sum of the kinetic and potential energy?
At the initial time, is the energy coming from the potential energy or the kinetic energy? What initial condition would make the energy all kinetic energy?
After two periods (as measured in the last part), is the energy mostly potential or kinetic? The answer, in retrospect, should be obvious.

(G2b) Critical Damping

(G2b.1) Set the damping coefficient alpha to 0.1, and run from our standard initial conditions (Theta 0.7 and ThetaDot zero), but for a longer time (maybe to 30, or 100 if your computer is fast). Notice the oscillations as they slowly die out. Set the damping coefficient to ten, and run for the same initial conditions. The motion here is qualitatively different from that seen for small alpha. In your writeup, answer what's the qualitative difference? (Hint: does the curve oscillate - ever cross zero - for alpha=10?) Combine Theta vs Time for alpha=0.1, 1.0, and 10.0 on the same graph (using ``Copy Graph'' and ``Steal Data'') and include it in your writeup.

Notice that for large damping and for small damping you needed to run for a long time to see the decay, but for intermediate damping, the decay is quite a bit faster!

(G2b.2) Roughly find out (to better than one significant figure) at what value of alpha the oscillations stop. Include your value in the lab writeup. This is called critical damping. Putting the damping just large enough to kill the oscillations also removes the energy as fast as possible: making the damping even larger is counterproductive.

(G2b.3) Imagine our pendulum is a screen door, with the ball at the end representing the doorknob, and the pivot of the pendulum representing the hinge. Screen doors are often attached with springs - dissipation is low, so they are roughly described by the harmonic pendulum equation with alpha=0. Spring-attached screens slam when they close: when the pendulum reaches Theta=0 it hits the door frame hard. There are fancier gizmos to pull screen doors shut, that we can model as a dashpot filled with oil - well described by our damped equation of motion above, with alpha > 0. What value of alpha best balances the need to shut the door fast (avoiding mosquitos), without slamming? Are the two needs incompatible?

Damping occurs in most physical systems. Sound is damped in air, light is absorbed as it passes through water, guitar strings don't vibrate forever. The wave equation we study in this course as a model for these systems ignores this damping. This is in many circumstances an excellent approximation, and furthermore ignoring this complication allows us to study the fascinating concepts of wave propogation, interference, and diffraction more simply and clearly - just like ignoring air friction allowed Newton to understand trajectory motion more clearly.

Links Back

Statistical Mechanics: Entropy, Order Parameters, and Complexity, now available at Oxford University Press (USA, Europe).