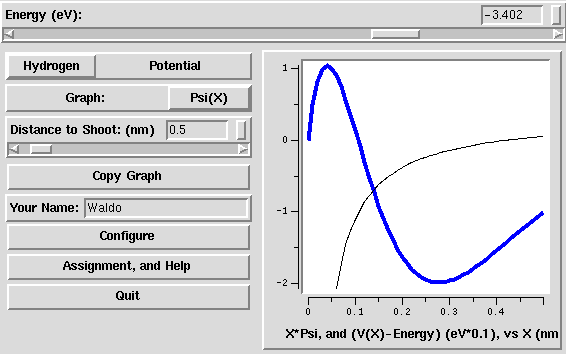

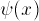 , as a
function of position x (in nm). For the two square well potentials,
it can show either
, as a
function of position x (in nm). For the two square well potentials,
it can show either 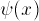 or the probability
distribution
or the probability
distribution 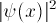 (see Graph below). For
the Hydrogen potential, it shows
(see Graph below). For
the Hydrogen potential, it shows 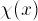 or its square,
where the three-dimensional Hydrogen electron wave-function
is given by
or its square,
where the three-dimensional Hydrogen electron wave-function
is given by 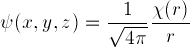 (see
section 3 of the lab).
For the square-shelf potential, and for the Hydrogen potential, it also
shows the potential energy V(x), but somewhat rescaled: it
subtracts the energy of the wave-function, and multiplies by a factor
(default 0.1). Subtracting the energy E is useful because only
V(x)-E comes into the Schrödinger equation: in particular, the
wave function oscillates whenever V(x)-E < 0 and grows
or decays exponentially whenever V(x)-E > 0.
(see
section 3 of the lab).
For the square-shelf potential, and for the Hydrogen potential, it also
shows the potential energy V(x), but somewhat rescaled: it
subtracts the energy of the wave-function, and multiplies by a factor
(default 0.1). Subtracting the energy E is useful because only
V(x)-E comes into the Schrödinger equation: in particular, the
wave function oscillates whenever V(x)-E < 0 and grows
or decays exponentially whenever V(x)-E > 0.
You can vary the energy by
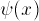 , or
, or
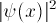 .
.
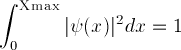
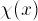 is used instead
of
is used instead
of 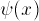 , and the normalization is not correct (see Hydrogen
above).
, and the normalization is not correct (see Hydrogen
above).
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).