S3: Hydrogen
The Hydrogen atom consists of a proton at the nucleus and an electron
in a cloud surrounding it. Because the proton is so much heavier than
the electron, we think of the electron as sitting in a potential well
due to the proton: if the electron is a distance r from the
proton, there is a Coulomb energy
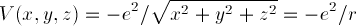
holding the electron to the proton.
How can we solve this problem? To solve it, we need to solve
for a three-dimensional wave function 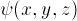 ;
we only know how to solve Schrödinger's equation in one
dimension! It turns out that one can break up the problem,
solving the radial part of the equation separately from the
angular dependence. It so happens that a slightly different
function
;
we only know how to solve Schrödinger's equation in one
dimension! It turns out that one can break up the problem,
solving the radial part of the equation separately from the
angular dependence. It so happens that a slightly different
function 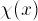 can be defined,
can be defined,
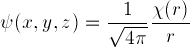
which satisfies exactly our one-dimensional Schrödinger equation:
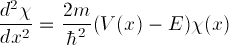 .
.
The boundary conditions also remain the same:
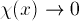 as
as 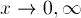 .
How convenient!
.
How convenient!
We won't go into the angular parts of Hydrogen's wave equation in this course.
For the chemists among us, the angular parts give the differences between
the s, p, and d states.
Our wavefunctions 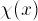 , when divided by r,
will give exactly the 1s, 2s,
3s, 4s, 5s, and
6s states. It happens (for truly obscure reasons)
that the energies of the p and d states
are the same as the energies for the s states, so
we can compare the energies we numerically calculate in this lab directly to
those we will measure in the experimental Spectrum of
Hydrogen lab. We'll label our states, instead of
1s, by their energies E1, E2, ....
, when divided by r,
will give exactly the 1s, 2s,
3s, 4s, 5s, and
6s states. It happens (for truly obscure reasons)
that the energies of the p and d states
are the same as the energies for the s states, so
we can compare the energies we numerically calculate in this lab directly to
those we will measure in the experimental Spectrum of
Hydrogen lab. We'll label our states, instead of
1s, by their energies E1, E2, ....
(S3a) The Ground State
Find the energy of the ground state of hydrogen. Change the potential
type to Hydrogen. Note that the black line now shows the hydrogenic
potential energy, and that the range has shrunk to 0.5nm.
You should start in the region between -13eV and -14eV, and then zero in
on a good value. Note that the energies in this section are
negative! This is just because of the convention for the Coulomb
potential: V(x) can't be set to zero at zero (why?) so we
set it to zero at infinity.
(You can see the hints for
the Energy slider for tips on zooming in efficiently.)
You should be able to get the energy to five significant figures
(-13.XXX). (The last decimal place isn't correct, actually: you can
hit Configure and make delta_x half
the size to get a better number if you're ambitious.) Include
the ground-state energy in your writeup, and sketch
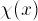 for the ground state. The ground
state is also called the 1s state, and we'll
call its energy E1.
for the ground state. The ground
state is also called the 1s state, and we'll
call its energy E1.
(S3b) The Excited States
Find the energies of the first three excited states (four states in all).
As you sweep the energy, every time the tail whips from up to down
or down to up you've passed an eigenstate. You should be able to
tell if you've missed a state by counting the nodes in the wave-function.
Be careful
- to expand the Distance to Shoot each time you
raise the energy. You want to make sure at least the right-most third of the
graph is showing the exponential growth or decay, so that you can kill
it carefully,
- in counting nodes, not to count the one which - for the exact
solution - would be at infinity: if the tail of the wave-function
diverges in the wrong direction your approximate wave-function might show
that node in the tail,
- to get at least two significant figures after the decimal point.
Include these energies in your writeup, and label them
E2, E3, as appropriate. Sketch in your
lab notebook the function 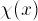 for the energy
E3 (the second excited state), over the range
0 < X < 2.5nm, or (if your TA prefers) use the ``Copy
Graph'' button to save the PostScript file, print it, and include that
in your writeup.
for the energy
E3 (the second excited state), over the range
0 < X < 2.5nm, or (if your TA prefers) use the ``Copy
Graph'' button to save the PostScript file, print it, and include that
in your writeup.
(S3c) The Energy Level Diagram
As in part 1, draw an energy level
diagram in your writeup for the first four energy states of the
hydrogen atom, leaving room at the top for states between the highest
energy you found and E=0. Plot the energies to scale! (This
should occupy the entire length of a sheet of paper.) You should find
that they form a simple pattern, bunching up as they approach the top of
the Hydrogen potential well at E=0. Label the states with their
energies in eV, and with their numbers E1, E2, ...
(S3d) Comparing to the Answer
It's rare in quantum mechanics that one can find solutions to the
equations. The hydrogen atom is one of those rare cases: the
energies for the states (and the wave-functions) can be found
exactly (ignoring relativistic effects). In your writeup,
compare the first four
energies you found to the exact formula
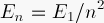
How close did we come? Use the formula and your ground-state energy
to predict where the next two energy states should lie. Type in
these energies, and verify that your predictions are close to the
next two energy states in the ladder. Add them to your
energy level diagram.
(S3e) The Visible Spectrum of Hydrogen
Look back to the end of part 1 to review
how to get the frequencies of the emitted light, given the
energy differences between the initial state of the electron and
the final state. Is the light emitted from the transition from
the first excited state to the ground state in the visible range?
How about the transition from En to E1, for n> 2?
In the experimental Spectrum of Hydrogen lab, we'll
measure several visible lines, which will turn out to be transitions
into the first excited state E2, from the levels E3, ... E6.
(These are the Balmer lines. The inventors of quantum mechanics used
these lines to guess the equations: it's like listening to a violin
string and deducing the wave equation.)
Using your measured values, predict the frequencies
(in cycles/sec) and the wavelengths for these four transitions. What
colors should the light be?
We will measure precisely these four lines (if your eyes are good) in the
experimental Spectrum of Hydrogen lab. Include the predicted
colors and frequencies in your writeup, and also jot them down on a
separate piece of paper to bring to the experimental lab session!
Links Back
- Infinite Square Well
- Square Shelf
- Hydrogen
 Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
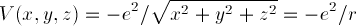
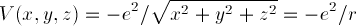
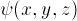 ;
we only know how to solve Schrödinger's equation in one
dimension! It turns out that one can break up the problem,
solving the radial part of the equation separately from the
angular dependence. It so happens that a slightly different
function
;
we only know how to solve Schrödinger's equation in one
dimension! It turns out that one can break up the problem,
solving the radial part of the equation separately from the
angular dependence. It so happens that a slightly different
function 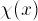 can be defined,
can be defined,
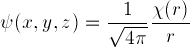
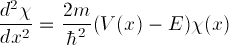 .
.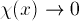 as
as 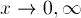 .
How convenient!
.
How convenient!
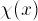 , when divided by r,
will give exactly the 1s, 2s,
3s, 4s, 5s, and
6s states. It happens (for truly obscure reasons)
that the energies of the p and d states
are the same as the energies for the s states, so
we can compare the energies we numerically calculate in this lab directly to
those we will measure in the experimental Spectrum of
Hydrogen lab. We'll label our states, instead of
1s, by their energies E1, E2, ....
, when divided by r,
will give exactly the 1s, 2s,
3s, 4s, 5s, and
6s states. It happens (for truly obscure reasons)
that the energies of the p and d states
are the same as the energies for the s states, so
we can compare the energies we numerically calculate in this lab directly to
those we will measure in the experimental Spectrum of
Hydrogen lab. We'll label our states, instead of
1s, by their energies E1, E2, ....
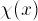 for the ground state. The ground
state is also called the 1s state, and we'll
call its energy E1.
for the ground state. The ground
state is also called the 1s state, and we'll
call its energy E1.
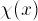 for the energy
E3 (the second excited state), over the range
0 < X < 2.5nm, or (if your TA prefers) use the ``Copy
Graph'' button to save the PostScript file, print it, and include that
in your writeup.
for the energy
E3 (the second excited state), over the range
0 < X < 2.5nm, or (if your TA prefers) use the ``Copy
Graph'' button to save the PostScript file, print it, and include that
in your writeup.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).