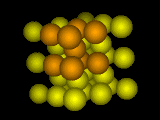
Hot ... turns to
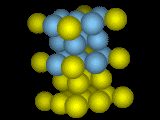Cold (or cold to hot, for steels).
What crystal structure a given element will form is a subtle and complicated question. A few general guidelines are known. Simple cubic crystals with only one element are rare, mostly because they're floppy and tend to distort. Body-centered cubic (bcc) packings of atoms tend to be most stable near the melting point because the atoms have room to vibrate (important at high temperatures): face-centered cubic (fcc) crystals are common among metals at low temperatures because the atoms pack well. Steels, perversely, are body-centered cubic at low temperatures and face-centered cubic at high temperatures. When you consider compounds or alloys made of more than one element, the variety of different crystal structures seen is quite bewildering.
What happens, then, when the atoms change their mind? If a material likes to be body-centered at high temperatures, and face-centered at low temperatures, how does the material get from one state to the other? In this case, and in many other transitions from one crystal structure to another, the transformation needn't break all the bonds and start over: one crystal structure can smoothly deform into the other by a shear deformation: expanding in one direction and squeezing in the other two.
Hot ... turns to
Cold (or cold to hot, for steels).
Transformation from Body-Centered to Face Centered by Stretching Vertically.
Things get complicated, though, because there's more than one way to stretch! We could just as well have stretched along one of the other two axes for bcc ... leading to two other rotated fcc phases.
or
For steels, you need to choose the various bcc squashed crystals from a single fcc high-temperature phase, but otherwise it's similar.
We'll model this system with a simpler, two dimensional system. Our two-dimensional transition will go from a square, high temperature phase to a rectangular phase: either short-and-fat (orange) or tall-and-thin (cyan, or blue).
Hot ... turns to
Cold.
These shape changing transformations happen in the real world. When a blacksmith hammers on a horseshoe, he (or she?) heats it to red hot because it's softer there and easier to hammer. Why is it softer? When she plunges the shoe into a pail of dirty water, the crystal structure in the steel changes! The steel becomes harder (in part) because of this transformation.
If the steel in the horseshoe stretches in one direction and shrinks in two, does that mean the blacksmith has to hammer the horseshoe funny so it'll fit after it cools? No, the horseshoe overall doesn't change shape. Different regions in the horseshoe stretch in different directions: overall the horseshoe stays the same shape as the horse hoof. This happens to keep large strains from building up during the shape transformation. The boundaries between these different domains can be seen with a microscope, and form fascinating patterns of regular, parallel stripes.
Tom Shield at the University of Minnesota has some experiments showing martensitic patterns and the dynamics of the transformation (e.g., first movie, of Ni2MnGa below). Chunhwa Chu and Dick James also at the U of M have taken some great pictures of twin domains in martensites (second two pictures):
This characteristic pattern or microstructure was first seen by a German microscopist Adolf Martens around 1890, and materials with it are called martensites.
The transformation from one crystal shape to the other isn't nice and smooth: it happens in bursts, and in a complicated way. We hope you weren't misled by the smooth shift from bcc to fcc in the animations above! The system likes both the cubic arrangements, but doesn't like the intermediate strained arrangements. Watch the local regions jump from square to one of the rectangular shapes in this animation:
The funny cross-hatched patterns you see between the square phase and the striped martensite phase are called "tweed" (after the fabric). We've been studying these tweed patterns in much detail...
Entertaining Science done at
LASSP.
Jim Sethna,
sethna@lassp.cornell.edu
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).