Hysteresis is the history dependence of a material under an external strain. If one bends a table fork too far, it won't spring back to its original shape: past the elastic limit, the fork exhibits hysteresis. Unlike forks, which suffer damage (repeated cycles introduce work hardening and eventual fracture), many hysteretic systems will return to precisely the same state after being cycled. Magnetic tapes can be re-recorded, shape memory alloys can be cycled, vortex clusters can enter and leave superconductors, leaving the system in largely the same state it began in.

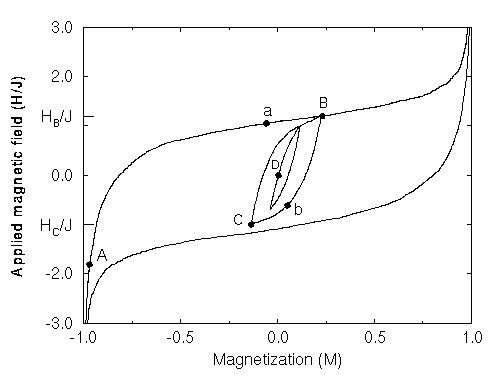
Hysteresis Loop Showing Return--Point Memory. Note that the system returns to the original curve at exactly the same state B that it left, that the returning curve has an apparent slope discontinuity at B, and that both effects also happen for the internal subloop. Thus a state can have a whole hierarchy of parent states (mothers at increasing fields and fathers at decreasing fields), which are seen as kinks in the corresponding branch of the H(M) curve.
This return--point memory effect is also known as ``wiping out'', since the memory of the excursion is wiped from the behavior of the material as soon as the field is raised past the previous extreme value. Subloops closing may not seem such a big deal, but some experimental acoustic emission data shown to me in Barcelona (taken originally in Mallorca), showed that every crackle and pop reproduces under cycling!
Return Point Memory: Experiment. Acoustic emission from a Cu-Zn-Al alloy, measured during thermal cycling through the martensitic transformation (traveling repeatedly around the hysteresis loop). A tiny portion of the two hysteresis loops is shown. Notice the sharp spikes from the various pulses (avalanches); notice the wide spectrum of avalanche sizes. Notice the excellent reproduction of even the fine structure when the loop is repeated. From Amengual et al., Thermochimica Acta 116, 195 (1987).
Sivan Kartha and I started modeling this system, and came up with a rather simple explanation of this unusual effect (it follows from partial ordering, no passing, and adiabaticity (Ref. 66)). We then addressed the question of why the popping, crackling sounds come in such a spectrum of sizes...
![]() James P. Sethna, sethna@lassp.cornell.edu
James P. Sethna, sethna@lassp.cornell.edu
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).