Particle physics and condensed-matter physics have quite different philosophies. Particle physicists are constantly looking for the building blocks. Once pions and protons were discovered to be made of quarks, they became demoted into engineering problems. Now that quarks and electrons and photons are made of strings, and strings are hard to study (at least experimentally), there is great anguish in the high-energy community. Condensed-matter physicists, on the other hand, try to understand why messy combinations of zillions of electrons and nuclei do such interesting simple things. To them, the fundamental question is not discovering the underlying quantum mechanical laws, but in understanding and explaining the new laws that emerge when many particles interact.
As one might guess, we don't keep track of all the electrons and protons. We're always looking for the important variables, the important degrees of freedom. In a crystal, the important variables are the motions of the atoms away from their lattice positions. In a magnet, the important variable is the local direction of the magnetization (an arrow pointing to the ``north'' end of the local magnet). The local magnetization comes from complicated interactions between the electrons, and is partly due to the little magnets attached to each electron and partly due to the way the electrons dance around in the material: these details are for many purposes unimportant.
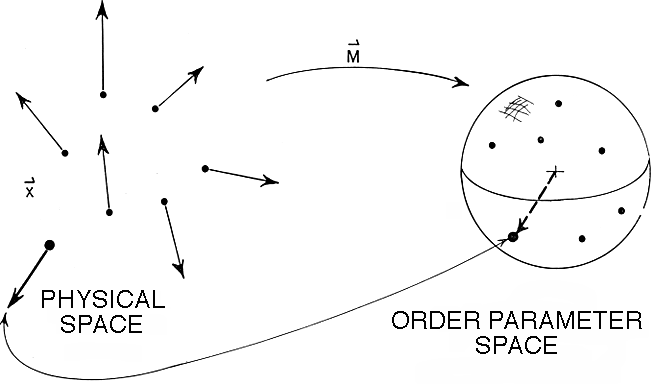
The important variables are combined into an order parameter field. In figure 4, we see the order parameter field for a magnet. At each position x=(x,y,z) we have a direction for the local magnetization M(x). The length of M is pretty much fixed by the material, but the direction of the magnetization is undetermined. By becoming a magnet, this material has broken the rotational symmetry. The order parameter M labels which of the various broken symmetry directions the material has chosen.
Figure 4. Magnet.
We take the magnetization M as the order parameter for
a magnet. For a given material at a given temperature, the amount of
magnetization |M| = M0 will be pretty well fixed, but
the energy is often pretty much independent of the direction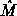 
=
M / M0 of the magnetization. (You can think of this
as a arrow pointing to the north end of each atomic magnet.) Often, the
magnetization changes directions smoothly in different parts of the
material. (That's why not all pieces of iron are magnetic!) We
describe the current state of the material by an order parameter field
M(x).
The order parameter field is usually thought of as an arrow at each
point in space. It can also be thought of as a function taking points
in space x into points on the sphere
|M| = M0. This sphere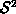 
is the order
parameter space for the magnet.
The order parameter is a field: at each point in our magnet, M(x) tells the local direction of the field near x. Why do we do this? Why would the magnetization point in different directions in different parts of the magnet? Usually, the material has lowest energy when the order parameter field is uniform, when the symmetry is broken in the same way throughout space. In practise, though, the material often doesn't break symmetry uniformly. Most pieces of iron don't appear magnetic, simply because the local magnetization points in different directions at different places. The magnetization is already there at the atomic level: to make a magnet, you pound the different domains until they line up. We'll see in this lecture that most of the interesting behavior we can study involves the way the order parameter varies in space.
The order parameter field M(x) can be usefully visualized in
two different ways. On the one hand, one can think of a little vector
attached to each point in space. On the other hand, we can think of
it as a mapping from real space into order parameter space. That is,
M is a function which takes different points in the magnet
onto the surface of a sphere (figure 4). Mathematicians call the
sphere 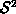, because it locally has two dimensions. (They don't care
what dimension the sphere is embedded in.)
Before varying our order parameter in space, let's develop a few more
examples. The liquid crystal in LCD displays (like those in digital
watches) are nematics. Nematics are made of long, thin molecules which
tend to line up so that their long axes are parallel. Nematic liquid
crystals, like magnets, break the rotational symmetry. Unlike magnets,
though, the main interaction isn't to line up the north poles, but to
line up the axes. (Think of the molecules as American footballs: the same
up and down.) Thus the order parameter isn't a vector M but a
headless vector n 
-n. The order
parameter space is a hemisphere, with opposing points along the equator
identified (figure 5). This space is called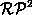 
by the
mathematicians (the projective plane), for obscure reasons.
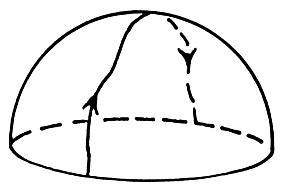
Nematic liquid crystal.
Nematic liquid crystals are made up of long, thin molecules that prefer
to align with one another. (Liquid crystal watches are made of nematics.)
Since they don't care much which end is up, their order parameter isn't
precisely the vector n along the axis of the molecules. Rather,
it is a unit vector up to the equivalence n-n.
The order parameter space is a half-sphere, with antipodal points on the equator
identified. Thus, for example, the path shown over the top of the
hemisphere is a closed loop: the two intersections with the equator
correspond to the same orientations of the nematic molecules in space.
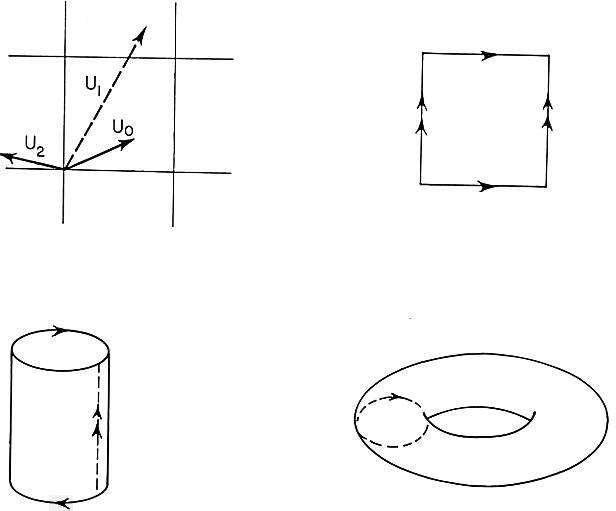
For a crystal, the important degrees of freedom are associated with the broken translational order. Consider a two-dimensional crystal which has lowest energy when in a square lattice, but which is deformed away from that configuration (figure 6). This deformation is described by an arrow connecting the undeformed ideal lattice points with the actual positions of the atoms. If we are a bit more careful, we say that u(x) is that displacement needed to align the ideal lattice in the local region onto the real one. By saying it this way, u is also defined between the lattice positions: there still is a best displacement which locally lines up the two lattices.
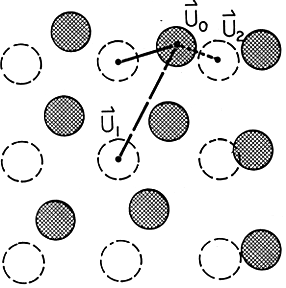
Figure 6. Two dimensional crystal.
A crystal consists atoms arranged in regular, repeating rows and
columns. At high temperatures, or when the crystal is deformed or
defective, the atoms will be displaced from their lattice positions.
The displacements u are shown. Even better, one can
think of u(x) as the local translation
needed to bring the ideal lattice into registry with atoms in the local
neighborhood of x.
Also shown is the ambiguity in the definition of u.
Which ``ideal'' atom should we identify with a given ``real'' one? This
ambiguity makes the order parameter u equivalent to
u + (m a,n a). Instead of a
vector in two dimensional space, the order parameter space is a square
with periodic boundary conditions.
The order parameter u isn't really a vector: there is a subtlety. In general, which ideal atom you associate with a given real one is ambiguous. As shown in figure 6, the displacement vector u changes by a multiple of the lattice constant a when we choose a different reference atom:
u
u + (m a,n a). (1)
The set of distinct order parameters forms a square with periodic boundary
conditions. As figure 7 shows, a square with periodic boundary conditions
has the same topology as a torus,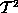 
. (The torus is
the surface of a doughnut, bagel, or inner tube.)
Order parameter space for a two-dimensional crystal.
Here we see that a square with periodic boundary conditions is a torus.
(A torus is a surface of a doughnut, inner tube, or bagel, depending
on your background.)
Finally, let's mention that guessing the order parameter (or the broken
symmetry) isn't always so straightforward. For example, it took many
years before anyone figured out that the order parameter for
superconductors and superfluid Helium 4 is a complex number
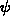. The order parameter field
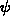(x) represents the ``condensate wave
function'', which (extremely loosely) is a single quantum state occupied
by a large fraction of the Cooper pairs or helium atoms in the material.
The corresponding broken symmetry is closely related to the number of
particles. In ``symmetric'', normal liquid helium, the local number of
atoms is conserved: in superfluid helium, the local number of atoms
becomes indeterminate! (This is because many of the atoms are condensed
into that delocalized wave function.) Anyhow, the magnitude of the
complex number 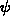is a fixed function of temperature,
so the order parameter space is the set of complex numbers of magnitude
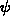||. Thus the order parameter space for
superconductors and superfluids is a circle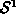 
.
Now we examine small deformations away from a uniform order parameter field.
Jim Sethna, sethna@lassp.cornell.edu
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).