Introduction to the simulation ``pythag''
The program pythag should start up with a pulse coming in from the left.
The pulse will travel down the string, bouncing off the ends, rather
like the wave on the spring in lecture (although slowed down a bit).
The large plot gives plots versus X, the small plot gives plots versus
time at the point represented by a dark rectangle on the large plot.
At several places in the lab, you will be asked to measure things about the
pulse. Let's begin by getting quick and accurate with these measurements.
- Stop the pulse at some place not close to one of the boundaries.
- Measure the amplitude of the pulse, by zooming in to the peak. You
can zoom by dragging with the right mouse button, or (if you only have
one button!) Control and dragging with the left or only button. Notice
that after zooming a few times you can see the discrete line segments
that the computer uses to approximate the curve. You should be able to
get the height of the pulse to at least four significant figures without
effort: you can use the left (or only) mouse button to read off the
position of a data point. Unzoom by clicking without dragging (either
right-click or control-click with the left or only button) in the
graphics window.
- Measure the position of the pulse. The best way to do this is to
change the graph from Y vs. X to
Y DOT vs. X: the peak position is where Y DOT crosses
zero. (You'll find it's much easier to measure where a line crosses zero
than where the peak of a hill is.) You should be able to measure the
position of the pulse to three significant figures.
- Measure the width of the pulse. In the lectures and problem sets,
we often talk about ``ball-park'' estimates of wave properties, based
on the ``pulse width''
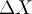 and the pulse height
A. It's clear what A should mean,
but what's the width of a pulse that slowly tapers off? Let us
agree here that
and the pulse height
A. It's clear what A should mean,
but what's the width of a pulse that slowly tapers off? Let us
agree here that 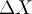 will stand for the ``full width
half maximum'': measure the x-positions of the two places where the pulse
crosses A/2, and the difference between these
two half-maxima is
will stand for the ``full width
half maximum'': measure the x-positions of the two places where the pulse
crosses A/2, and the difference between these
two half-maxima is 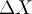 .
.
- The pulse takes a while to enter the string. Measure the time it takes
for the middle of the pulse (where Y DOT is zero) to reach X=0. (This
will be useful at several places in the lab.) To narrow in on the right
spot, you can either restart from scratch each time
- enter a new choice for ``Time to Run''
- hit ``Initialize'' to restart at zero time
- hit ``Run'', and see how close dy/dx(0) is to zero
or you can incrementally approach the crossing by typing in smaller and
smaller ``Time to Run'' (positive or negative!) and not re-initializing
in between. Don't bother with more than four decimal places.
Write this time down
somewhere.
You can check whether you measured the right value of the amplitude
A by hitting the Configure button: the amplitude
is listed in the upper left corner. This window also tells you most
of the other variables in the program: the length L of the string is
10 meters, the tension tau is 160 Newtons, the mass per unit length
Mu1 is 0.1 kg/meter
(Mu2 and Mu3 are discussed later). Notice that you did not get the
same value of the FWHM as shown in the Configure window: why? We'll
return to this in the next section.
Links Back
- Traveling Pulse
- Energy and Power
- Boundary Conditions and Colliding Pulses
- Reflection and Transmission
- Resonance
- Reflectionless Coatings
 Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
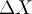 and the pulse height
A. It's clear what A should mean,
but what's the width of a pulse that slowly tapers off? Let us
agree here that
and the pulse height
A. It's clear what A should mean,
but what's the width of a pulse that slowly tapers off? Let us
agree here that 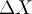 will stand for the ``full width
half maximum'': measure the x-positions of the two places where the pulse
crosses A/2, and the difference between these
two half-maxima is
will stand for the ``full width
half maximum'': measure the x-positions of the two places where the pulse
crosses A/2, and the difference between these
two half-maxima is 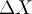 .
.