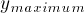P5: Resonance

Adapted from Joe Rogers, Fall 1996

If you have limited time at the computer, you can do parts (a) and (c) first, and part (b) later...

(P5a) Waves, Forcing, and Resonance

Start up the program pythag in the default configuration, set the left boundary Forcing to Wave, Initialize, and Run. This shows the kind of forcing we will be using in this problem: the left boundary is wiggled up and down with an amplitude 0.05 m at a frequency omega:

y(0,t)- (0.05 m) sin(omega t)

(except that the sine wave is made to turn on slowly, in order that the curve doesn't develop any kinks.)

Now load the preset OffRes. Launch the Configure menu, and notice that we've lowered the frequency by a factor of ten, to omega=30 radians/sec. Notice that the vertical scales on the plots are expanded, so the amplitude 0.05 of the forcing is now a small fraction of the range. Notice that the wiggles build up a bit, but don't keep growing.

Calculate the frequency omega of the lowest frequency standing wave in this simulation. Show your calculation in your solution, and enter this frequency in the Configure window under Omega. (If you're insecure about your answer, you can check it with the preset Reson.) Run for the full time (2.8 seconds). Forcing the boundary at a resonant frequency produces a large response (as you will see or perhaps have seen in the Tacoma Narrows Bridge video).

Make a table of the times at which y reaches a maximum and the value of y at each maximum by reading these from the Y vs. T graph. (Clicking the mouse on a point should show the numbers: don't bother zooming and such.) Leave room in your graph for two more columns. On what kind of curve do your 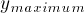versus t points fall? Explain why they should fall on this kind of curve.

(P5b) Total Energy, Average Power, and Power Input

We want to find out how fast the string is gaining energy. Add another column to your table for the total energy U. At the times when the displacement reached its maximum, the displacement was approximately a sine function with

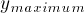in the middle and zero at the ends. Write out this function and use it to calculate the total energy as a function of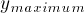

(Hint: why don't you need the kinetic energy density?) Fill in the total energy column U, by computing it using your formula and your values from the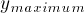

column in your table. Now find the average power entering the string during the past oscillation

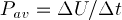and enter that into a fourth column for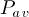

. Sketch a graph of U and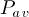

as a function of t. Is

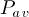constant, or is it increasing linearly with time? Explain why it behaves that way in terms of the equation for the power entering the left end of the string:

(P5c) Off Resonance

Initialize the program again, but this time enter a frequency omega which is 30% or 40% larger, and run the program. Describe what you see and explain why it is different from what you saw in the first part of this problem.

Links Back

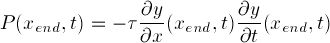
Statistical Mechanics: Entropy, Order Parameters, and Complexity, now available at Oxford University Press (USA, Europe).