P2: Energy and Power for a Traveling Pulse
(P2a) Energies and Energy Density
The total energy U for a wave y(x,t) on a string
is the integral of the energy density u(x) over the string, where

the first term under the integral is the potential energy density
of the spring, and the second term is the kinetic energy density.
One can estimate the energy in a boring, simple,
structureless, up-and-down pulse
like the one studied here, simply from dimensional analysis.
Make a table with four columns and the following three rows:
- potential energy density
- kinetic energy density
- energy density
If you use the amplitude A for all the dy's in the formula, the
pulse length in space for all the dx's, and the pulse length in
time for the dt's, you can write an algebraic formula for each of
these quantities in terms of A, 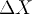 ,
, 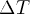 ,
and the string parameters tau, Mu1, and L. Put these formulas
in the first column of the table.
,
and the string parameters tau, Mu1, and L. Put these formulas
in the first column of the table.
Evaluate the formulas using the parameters of our problem, and
enter these in the second column. For
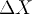 , you can either measure the FWHM, or you can
calculate it from
, you can either measure the FWHM, or you can
calculate it from 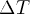 , tau, and mu.
, tau, and mu.
By selecting the relevant quantity to measure on the "vs X" plot,
measure rough peak numerical values for each of the three energy densities,
and fill these into the third column. What would you need
to do to get the total energies?
Dimensional analysis has its limitations. Suppose we use a wiggly
``Packet'' instead of the nice smooth ``Pulse''? Run a packet, and
in the fourth column, put the peak densities of the
three kinds of energies you found. Why is the energy density so far
from that predicted by dimensional analysis? Is there another way
to estimate the energy densities, if the wavelength of the modulation
is much smaller than the length of the packet?
Dimensional analysis doesn't work unless the objects really are described
well using the dimensions: our funny packet has an internal length much smaller
than the pulse width, so the local slope really isn't given by the
height of the packet divided by the length of the packet.
(P2b) Relationship between Potential and Kinetic Energy:
Traveling Wave
Using the fact that the pulse and packet are both traveling waves,
y(x,t) = f(x-vt)
derive a formula relating the potential energy density to
the kinetic energy density, and add it to your writeup. Does the Pulse
satisfy this? Does the Packet? Note each success and failure in your
writeup.
(P2c) Relationship between Energy and Power: Traveling Wave
Again using the traveling wave form, derive a formula
relating the energy density and the power, for your writeup. Using the
shapes and the peak values, compare the energy density and power for a
pulse moving to the right: is the ratio correct? Compare the energy density
and power for a pulse moving to the left: is it still OK? Compare the
energy density and power for a Packet. Note each success and failure
in your writeup.
The relationships in parts (b) and (c) are very useful, and apply
to all shapes of packets, but they only apply to traveling waves.
Links Back
- Traveling Pulse
- Energy and Power
- Boundary Conditions and Colliding Pulses
- Reflection and Transmission
- Resonance
- Reflectionless Coatings
 Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).


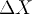 ,
, 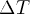 ,
and the string parameters tau, Mu1, and L. Put these formulas
in the first column of the table.
,
and the string parameters tau, Mu1, and L. Put these formulas
in the first column of the table.
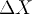 , you can either measure the FWHM, or you can
calculate it from
, you can either measure the FWHM, or you can
calculate it from 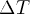 , tau, and mu.
, tau, and mu.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).