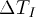 and the speed of sound V1 on the first segment of string,
find the FWHM width
and the speed of sound V1 on the first segment of string,
find the FWHM width 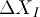 of the peak in space.
Include it in your writeup.
of the peak in space.
Include it in your writeup.
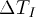 , and the amplitude
, and the amplitude 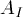 from the Configure menu; while you're
doing so, copy down the values for Mu1 and Mu2 for this preset.
from the Configure menu; while you're
doing so, copy down the values for Mu1 and Mu2 for this preset.
Either by measurement, or by calculation from the FWHM in time
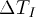 and the speed of sound V1 on the first segment of string,
find the FWHM width
and the speed of sound V1 on the first segment of string,
find the FWHM width 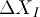 of the peak in space.
Include it in your writeup.
of the peak in space.
Include it in your writeup.
Measure the amplitude 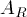 and the FWHM width
and the FWHM width
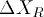 of the reflected pulse. Measure the amplitude
of the reflected pulse. Measure the amplitude
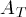 and the FWHM width
and the FWHM width 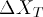 of the
transmitted pulse. Include these in your writeup.
of the
transmitted pulse. Include these in your writeup.
It's easy to calculate quantitatively the widths of the different pulses!
Calculate, using your measured widths 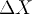 for the pulses and
using the speed of sound in the two media, the widths of the
transmitted and reflected pulses in time,
for the pulses and
using the speed of sound in the two media, the widths of the
transmitted and reflected pulses in time, 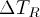 and
and
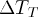 . They will agree. Include in your
writeup.
. They will agree. Include in your
writeup.
Why are they all the same? Think of the knot (the black rectangle) as exerting a force on the red string as the incident pulse hits it. Surely the force lasts just as long as the incident pulse lasts: hence the transmitted pulse must last the same time (and have the same overall shape) as the incident pulse! Similarly, the knot, pulled by the incident pulse, can reflect energy back only so long as the incident pulse is there: again, the times must agree.
Let's get a qualitative feeling for the amplitudes of the reflected and
transmitted pulses. Suppose the red string were extremely
light: it then would seem much the same as a free boundary condition
(how can wiggling a spider web thread put any significant force on a
rope?) The reflected pulse should thus look the same as that for a free
boundary condition. Does that agree with what you see? The incident
and reflected pulse off the spider thread will have the same height 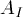 =
=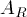 . When the incident pulse is
centered just on the knot, the knot on the blue rope is thus at Y =
. When the incident pulse is
centered just on the knot, the knot on the blue rope is thus at Y = 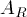 +
+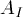 = 2
= 2 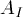 .
That means that the transmitted pulse will have twice the amplitude of
the incident pulse! Our Mu2 is one quarter of Mu1 (not really a thread);
is the amplitude of the transmitted pulse bigger than the incident? In
your writeup, explain how energy can be conserved, when
the transmitted pulse is both higher and longer!
.
That means that the transmitted pulse will have twice the amplitude of
the incident pulse! Our Mu2 is one quarter of Mu1 (not really a thread);
is the amplitude of the transmitted pulse bigger than the incident? In
your writeup, explain how energy can be conserved, when
the transmitted pulse is both higher and longer!
There are two equations that we will use in the homework to derive
a formula for the transmitted and reflected amplitudes for a step
jump in the mass density per unit length. Both involve the fact that
stuff from the red string and the blue string have to agree at the knot.
Since the peak of the transmitted and reflected pulses form at the knot
exactly when the incident pulse peaks there, and since the string can't
jump there (or it would break), we get an equation guaranteeing
the continuity of string:
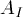 +
+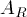 =
=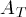 .
.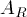 ,
, 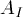 , and
, and 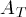 in this equation. To how many decimal places does your measurement
agree with it?
in this equation. To how many decimal places does your measurement
agree with it?
The second equation reflects the conservation of energy at the knot
between the two strings. Since the knot cannot absorb or emit energy,
the power flowing into the knot must be zero at all times. The power
coming into the knot from the blue rope is 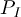 +
+
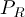 (remember
(remember 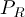 is
negative, so adding it to
is
negative, so adding it to 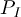 makes
makes
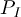 smaller reflecting the power
leaving the knot in the reflected pulse). The power leaving the
knot on the red string is
smaller reflecting the power
leaving the knot in the reflected pulse). The power leaving the
knot on the red string is 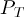 . So we get a conservation of energy
equation, yielding the balance of power:
. So we get a conservation of energy
equation, yielding the balance of power:
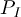 +
+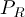 =
=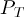
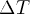 ,
widths in space
,
widths in space 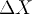 , and peak powers P for the incident,
transmitted and reflected waves. Include into your writeup.
, and peak powers P for the incident,
transmitted and reflected waves. Include into your writeup.
Make sure the 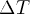 's are the same, as before. Check that the
continuity-of-string equation is satisfied. Include both into your
writeup.
's are the same, as before. Check that the
continuity-of-string equation is satisfied. Include both into your
writeup.
Explain qualitatively the amplitude of the reflected pulse, by thinking about the limit where the second rope becomes infinitely massive. Figure out the kind of boundary condition you would expect the blue string to see at the knot in this limit, and include in your writeup. For this boundary condition, what is the sign and amplitude of the reflected pulse?
In the infinitely massive limit, what should be the amplitude of the transmitted pulse, according to the continuity-of-string equation above? Predict this in your writeup.
Verify that your StepUp measurements of the amplitudes satisfy the continuity-of-string equation, and that the measurements of the powers satisfy the conservation-of-energy equation: add to your writeup how many decimal places are satisfied for each equation according to your measurements.
Keep the measurements of the amplitudes, powers, time widths, and spatial widths for these two different mass densities: they will likely appear on problem set in the near future.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).