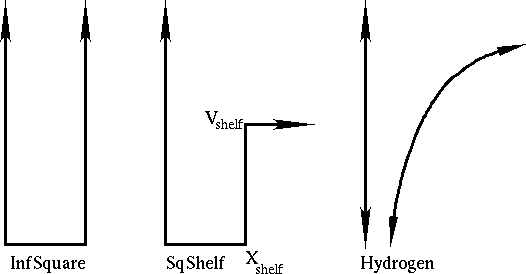
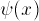 for an electron in
a potential, with definite energy given by the slider value.
In this lab, we will be finding solutions of definite energy which
satisfy the correct boundary conditions on the right. We'll do
this for three different potentials: the infinite square well,
the square-shelf potential, and the Coulomb potential for the
hydrogen atom.
for an electron in
a potential, with definite energy given by the slider value.
In this lab, we will be finding solutions of definite energy which
satisfy the correct boundary conditions on the right. We'll do
this for three different potentials: the infinite square well,
the square-shelf potential, and the Coulomb potential for the
hydrogen atom.

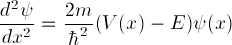 .
. is Planck's constant h divided by
two pi, and V(x) is a potential energy well.
We will be varying the energy E and looking for
well-behaved solutions.
is Planck's constant h divided by
two pi, and V(x) is a potential energy well.
We will be varying the energy E and looking for
well-behaved solutions.
This is a special form of the general, time dependent Schrödinger
equation
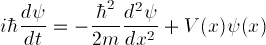 ,
,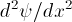 is
proportional to the wave function
is
proportional to the wave function 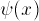 , just like the
second derivative of theta with respect to t was proportional
to theta.
, just like the
second derivative of theta with respect to t was proportional
to theta.
Many of you are familiar with electron wave-functions from chemistry.
There one describes, for example, s and p
states of various shapes, which can be occupied by the electron, binding
it to the nucleus. The shapes of these wave-functions in large part
determines the chemical bonding of the atoms. The energies of these
wave-functions determines the frequencies of the light they can absorb
and emit. Unlike waves on a string, each solution does not separately
resonate with light of a particular frequency.
Instead, light is emitted and absorbed when the electron
changes from one state to another, and the frequency of the
light is determined by the difference in energies between the two
solutions:
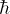
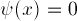 at X=0, and (depending on the
potential) either
at X=0, and (depending on the
potential) either
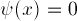 at X=Xshelf, or
at X=Xshelf, or
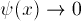 as X goes to infinity. Because
our boundary conditions involve two different points, this is an
example of a two-point boundary value problem.
as X goes to infinity. Because
our boundary conditions involve two different points, this is an
example of a two-point boundary value problem.
We'll solve the problem by "shooting": we pretend we know the derivative
of 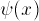 at X=0, solve the equation, and
then fiddle around until it has the right value at the other boundary.
For our problem, we'll fiddle around with the energy E:
raising and lowering the energy will change how the electron wave function
acts at the right-hand boundary.
at X=0, solve the equation, and
then fiddle around until it has the right value at the other boundary.
For our problem, we'll fiddle around with the energy E:
raising and lowering the energy will change how the electron wave function
acts at the right-hand boundary.
The default potential is a square well, with infinite walls. Try varying the energy to make the wave-function zero at the right-hand side! You'll find there are several solutions, with different numbers of nodes, just like there are several different shapes of wave-functions for electrons in your chemistry class.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).