S2: The Square Shelf Potential
Particle in a Box with One Infinite and One Finite Side
We now want to explore a situation where the particle not only
oscillates inside the box, but is (quantum-mechanically) allowed
to leak a bit outside the box. This problem is much harder
to solve analytically, but we can get
the main physical results from our numerical solution.
Change the Potential from InfSquare to
SquareShelf. Notice the thin black line,
which indicates the square-well potential. The height of the
step is shrunk by a factor of ten, so that it fits on the
graph: the energy V(x) for X > Xshelf
is Vshelf=3eV by default. Notice that we're plotting V(x)-E:
the thin black line is not at zero, and is not
the y-axis! This way, when the thin black line goes through
zero, V(x)-E changes sign, and the behavior of
Schrödinger's equation changes.
Try varying the energy. You'll find that the wave-function swings
wildly in the range above Xshelf. Investigate energies
between two and three for a while. Where V(x)=0,
notice that the wave-function oscillates up and down. On the shelf,
where V(x) < E, notice that the wave-function tends
to go crazy. Increase Distance to Shoot to
three: on the shelf, see that Psi either grows exponentially
to infinity or to minus infinity.
(S2a) Analytic Solutions for V-E>0
If V(x) is constant and greater than E,
we say the electron is in a ``classically forbidden'' region
(because it doesn't have enough energy to be there). We
can find solutions to Schrödinger's equation in the special
case where V(x)=V is a constant. Show, in your lab
writeup, that the time-independent Schrödinger equation
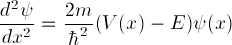
in this case has an exponentially growing solution
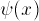 = A1 exp(B x) and an exponentially
decaying solution
= A1 exp(B x) and an exponentially
decaying solution
 = A2 exp(-B x). What is B, when
E=2.5eV? (Remember from part 1
that
= A2 exp(-B x). What is B, when
E=2.5eV? (Remember from part 1
that  =26.246 (eV^(-1) nm^(-2)).)
Express B in 1/nm (inverse nanometers), and include
in your lab writeup.
=26.246 (eV^(-1) nm^(-2)).)
Express B in 1/nm (inverse nanometers), and include
in your lab writeup.
(S2b) Numerical Solutions for V-E>0
Set Distance to Shoot to 3 nm, and
Energy to 2.5 eV (for the Square Shelf potential), and
Copy Graph. In the Configure menu of the copied graph, select Y Log.
Notice that the graph looks rather like a straight line on the shelf,
especially for X>2. (The funny chopped-up look in the well
comes from the program trying to take logarithms of negative numbers:
don't worry about it). Measure the value of Psi at 2 nm and 3 nm (by
using the left mouse button). How close is the ratio of Psi(2) to
Psi(3) to that predicted by your exponentially growing solution? You
should get agreement to within one percent: include the comparison
in your writeup.
Having  grow exponentially is not the correct
boundary condition! This may be obvious: if the electron doesn't
have enough energy to be there, it shouldn't zoom off further and
further into the forbidden zone. We can derive this formally
by noticing that the wave-function must be normalized.
Since the square of the wave-function at X gives the probability
density of finding the electron there, and the electron must be someplace
(and not more than one place), the integral of
grow exponentially is not the correct
boundary condition! This may be obvious: if the electron doesn't
have enough energy to be there, it shouldn't zoom off further and
further into the forbidden zone. We can derive this formally
by noticing that the wave-function must be normalized.
Since the square of the wave-function at X gives the probability
density of finding the electron there, and the electron must be someplace
(and not more than one place), the integral of 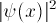 must be one:
must be one:
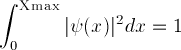
(Things are more subtle if the electron isn't bound in the well:
see S2e below).
This implies 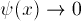 as X gets large:
we want the exponentially decaying solution.
as X gets large:
we want the exponentially decaying solution.
Even at E=2.5 eV the solution on the shelf is a mixture of
exponentially decaying and growing pieces: we had to look at
X>2 to see a straight line on the log plot because only there
was the exponentially decaying piece so small that it didn't show up.
Let's vary the energy until we remove the growing piece! Notice that for
E=2.6 eV the wave-function is exponentially growing downward: the
constant A1 multiplying A1 exp(B x) is negative.
Someplace between E=2.5 eV and 2.6 eV the constant
had to go to zero. At that point, 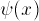 just has an
exponentially decaying piece, and the solution is physically sensible:
we have one of our energy states.
just has an
exponentially decaying piece, and the solution is physically sensible:
we have one of our energy states.
(S2c) Finding an Energy State
By varying the energy carefully, find the point between
E=2.5 and 2.6 eV where the exponentially growing
piece of the wave-function is smallest. Locate this point
to five significant figures (i.e., 2.5XXX), and include in your
writeup. (See the
help for Energy for hints
if you find zeroing in on the correct value tedious.)
Draw a picture of the wave-function in your writeup: also
draw a picture of the square of the wave function. How many
nodes (not including the one at zero, or the one that goes
to infinity as you get better and better energies) does this
solution have?
(S2d) Finding All the Bound States
Change Distance to Shoot back to 1.5 nm (the
exponential growth becomes so fast at lower energies that it's hard to
see what's happening), and look for the ground state solution. Raise
the energy and the range and find the other solutions. (Make the range
(shooting distance) large enough so you can be sure it's asymptoting in
the right way, but not so large that you can't control it at all.) How
many solutions can you find which are bound (go to zero as X
gets large)? You should find a solution with no nodes, one with one
node, ... up to the solution you found in part c. Draw
each solution in your writeup, and write down its energy.
(If your TA wants you to produce a hard-copy, use the ``Copy Graph'' and
``Steal Data'' buttons to generate a single graph with all the bound
states, making sure to fill the box for ``Your Name'' first.)
Draw an energy level diagram for the solutions you've found.
Did the energies shift up or down from those (with the same number of nodes)
you found in part 1?
The shelf potential resembles in some ways the potential for electrons
near a metal surface. As they leave the metal, the electron potential
jumps by the ``work function'' (famous because of its role in
the photoelectric effect, which we will likely cover in class).
There are lots of surface physics problems for which the exponentially
decaying electron wavefunction outside the surface has important
consequences... About how many nanometers does the ground-state
wave-function extend into the ``vacuum'' beyond Xshelf = 1 nm,
before the probability density decays to 1% of its peak value?
(S2e) Continuum States
There are also solutions to Schrödinger's equation which have
energies greater than Vshelf=3eV. They are unbound -
their wave-functions spread out everywhere, because they have enough
energy to escape from the well. (We can't use the normalization
condition for these solutions, since they are evenly spread out
over everything, but there are ways to fix that...) For V-E<0,
what should the wave-function do on the shelf? Change
Distance to Shoot to 4 nm, and observe the behavior as
you vary E between 3 eV and 5 eV. Draw a picture
in your writeup of the wave-function at E=4 eV.
Is the wave-length inside the well larger or smaller than outside?
Why? (That is, how does the wavelength depend on the size of
E-V?) What should the wave look like for energies much larger than
3 eV? Does the program look the same as your prediction?
(Note: energies bigger than 100 eV will start causing numerical problems...)
Links Back
- Infinite Square Well
- Square Shelf
- Hydrogen
 Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
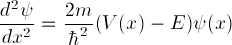
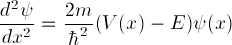
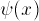 = A1 exp(B x) and an exponentially
decaying solution
= A1 exp(B x) and an exponentially
decaying solution
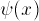 = A2 exp(-B x). What is B, when
E=2.5eV? (Remember from part 1
that
= A2 exp(-B x). What is B, when
E=2.5eV? (Remember from part 1
that  =26.246 (eV^(-1) nm^(-2)).)
Express B in 1/nm (inverse nanometers), and include
in your lab writeup.
=26.246 (eV^(-1) nm^(-2)).)
Express B in 1/nm (inverse nanometers), and include
in your lab writeup.
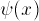 grow exponentially is not the correct
boundary condition! This may be obvious: if the electron doesn't
have enough energy to be there, it shouldn't zoom off further and
further into the forbidden zone. We can derive this formally
by noticing that the wave-function must be normalized.
Since the square of the wave-function at X gives the probability
density of finding the electron there, and the electron must be someplace
(and not more than one place), the integral of
grow exponentially is not the correct
boundary condition! This may be obvious: if the electron doesn't
have enough energy to be there, it shouldn't zoom off further and
further into the forbidden zone. We can derive this formally
by noticing that the wave-function must be normalized.
Since the square of the wave-function at X gives the probability
density of finding the electron there, and the electron must be someplace
(and not more than one place), the integral of 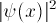 must be one:
must be one:
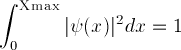
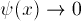 as X gets large:
we want the exponentially decaying solution.
as X gets large:
we want the exponentially decaying solution.
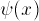 just has an
exponentially decaying piece, and the solution is physically sensible:
we have one of our energy states.
just has an
exponentially decaying piece, and the solution is physically sensible:
we have one of our energy states.
![]() Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).