S1: The Infinite Square Well
For the first portion of the lab, we will solve for the states of fixed
energy for a particularly simple potential: an infinite square well.
The potential V(x) is zero for 0 < X < Xshelf = 1nm,
and infinite everywhere else. (We call it Xshelf because it
will be the start of the shelf for the next section.)
Since the electron must be inside the box,
and the wave-function is continuous, we have the boundary conditions
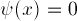 at both X=0 and X=Xshelf.
at both X=0 and X=Xshelf.
Since V(x)=0 inside the well, we are solving a familiar
equation: the second derivative of 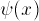 with respect
to X is a constant times
with respect
to X is a constant times 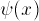 . We need to find
a solutions which vanish at the two ends. This is exactly the
same equation we solved for the simple harmonic oscillator, except we
have X instead of time t. It's also exactly the
same problem as solving for the standing waves on a string with fixed
boundary conditions.
. We need to find
a solutions which vanish at the two ends. This is exactly the
same equation we solved for the simple harmonic oscillator, except we
have X instead of time t. It's also exactly the
same problem as solving for the standing waves on a string with fixed
boundary conditions.
(S1a) Analytic Solutions
In your writeup, draw a picture of the ground state (the
lowest energy state, with the fewest antinodes). Either by following
the derivation in class, or by analogy
to the pendulum or the standing waves on a string, or by consulting your
text, calculate the energy of this lowest energy
state, as a formula involving m and 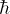 .
Draw pictures of the first three excited states, and
calculate their energies too. Include these in your
writeup.
.
Draw pictures of the first three excited states, and
calculate their energies too. Include these in your
writeup.
To evaluate your formulas for these energies, you'll need to figure out
 . You can do this in two different
ways. You need the answer in energy units of eV and length
units in nm (10^{-9} m). You can work everything out in eV:
the rest mass of the electron
. You can do this in two different
ways. You need the answer in energy units of eV and length
units in nm (10^{-9} m). You can work everything out in eV:
the rest mass of the electron
m c^2 = 0.511 MeV,
h = 4.1357x10^{-15} eV s, and
c = 2.997925x10^8 m/s.
Alternatively, you can work in MKS units:
m = 9.1095x10^{-31} kg,
h = 6.6262x10^{-34} J s, and
1 eV = 1.60219x10^{-19} J.
Remember that 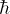 is h divided
by two pi.
is h divided
by two pi.
(S1b) Numerical Solutions
Using the program schrdgr, vary the energy to find values which make
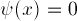 at X=1nm. Show that they
agree with the values you calculated, to at least three significant figures.
(You'll need to zoom in to your final point
to make sure the last few digits are correct.) Include
the comparison in your writeup: either show that the best
energies agree with your theoretical estimates, or that using your theory
numbers make the wavefunction vanish to the required accuracy.
at X=1nm. Show that they
agree with the values you calculated, to at least three significant figures.
(You'll need to zoom in to your final point
to make sure the last few digits are correct.) Include
the comparison in your writeup: either show that the best
energies agree with your theoretical estimates, or that using your theory
numbers make the wavefunction vanish to the required accuracy.
(S1c) Too low and too high energies.
Make a freehand sketch in your writeup of what happens to the
wave function when the ground state energy guess is a little too low.
Explain why this is true, using the Schrödinger equation
and discussing the curvature of the wave function and its dependence
on the energy E.
(S1d) Energy level diagram.
Draw in your writeup an energy level diagram.
This is pretty trivial: draw a vertical axis, label it E, and mark
with short (1 or 2cm) horizontal lines the values of the four
energies you derived. When the electron shifts from one
energy state En to another Em, a photon (a quantum particle of light)
is emitted, whose energy is En-Em, and whose frequency (in cycles
per second) is its energy divided by Planck's constant
h=4.1357 x 10^{-15} ev sec, and whose wavelength is
thus the frequency divided into the speed of light (3x10^{8}m/sec).
Will you be able to see light which is emitted when the electron
drops from the first excited state into the ground state?
What color will the light be when the electron drops from
the second excited state into the first excited state (i.e., level
3 into level 2 on your diagram)?
Links Back
- Infinite Square Well
- Square Shelf
- Hydrogen
 Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
Statistical Mechanics: Entropy, Order Parameters, and Complexity,
now available at
Oxford University Press
(USA,
Europe).
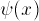 with respect
to X is a constant times
with respect
to X is a constant times 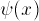 . We need to find
a solutions which vanish at the two ends. This is exactly the
same equation we solved for the simple harmonic oscillator, except we
have X instead of time t. It's also exactly the
same problem as solving for the standing waves on a string with fixed
boundary conditions.
. We need to find
a solutions which vanish at the two ends. This is exactly the
same equation we solved for the simple harmonic oscillator, except we
have X instead of time t. It's also exactly the
same problem as solving for the standing waves on a string with fixed
boundary conditions.
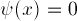 at both X=0 and X=Xshelf.
at both X=0 and X=Xshelf.
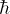 .
Draw pictures of the first three excited states, and
calculate their energies too. Include these in your
writeup.
.
Draw pictures of the first three excited states, and
calculate their energies too. Include these in your
writeup.
 . You can do this in two different
ways. You need the answer in energy units of eV and length
units in nm (10^{-9} m). You can work everything out in eV:
the rest mass of the electron
. You can do this in two different
ways. You need the answer in energy units of eV and length
units in nm (10^{-9} m). You can work everything out in eV:
the rest mass of the electron