What is Sloppiness?

 Scientific theories make predictions about the real world that depend upon our knowing certain parameters governing the behavior. Sometimes, like in Newton's laws, these parameters (the force due to gravity and the masses of the objects) are known. But in many cases, some or many of the parameters are either unknown or significantly uncertain. Our models of the reactions in a cell (systems biology), for example, involve many parameters describing how proteins interact with one another; none of these parameters have been measured well.

In other cases, we may want to vary parameters to change the system behavior. Physicists designing the next accelerator (the ILC) here at Cornell have a computer model of the entire beam line, with over 100 parameters. What combinations of parameters will give a good beam at low power and low cost? If the beam is bad in a certain way, which combinations of parameters can be used to fix it?

Parameter indeterminacy and sloppiness

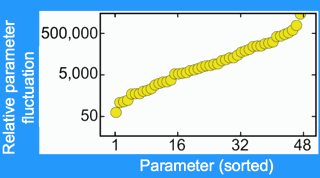
Parameter Ranges
Huge parameter variations. The factor by which each parameter can vary, keeping the system behavior fixed.

It's long been known that many multiparameter models are loosely constrained, or ill conditioned: many parameter sets can exhibit the same behavior. When we were exploring some problems in systems biology, though, we were startled by the giant ranges of parameters that could still fit the data. Each of the parameters in our model could vary by at least a factor of fifty, and many by factors of thousands (left) without changing the behavior. And yet, the model was useful - these widely varying parameters sets agreed for many important predictions.

Calling a model like this "loosely constrained" is like calling the ocean wet. We call these sloppy models. We emphasize, though, that one should think of sloppiness not as a failure of the model! Some of the most precise calculations in physics (variational wavefunctions used in quantum Monte Carlo for high-accuracy molecular energy calculations) are sloppy. We shall see that sloppiness is often compatible with good predictive power, for most everything of interest except the parameters.

 

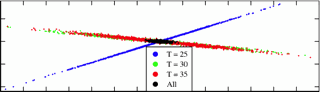
Three thin colored regions intersecting at black blob
Sloppy parameter regions, at three temperatures for a model of circadian rhythms. The colored dots show regions where the model behavior fits experiment at each temperature; the black dots show 'robust' behavior where the model works at all temperatures (see Environmental robustness and sloppiness).

The behavior of sloppy multiparameter models does depend on the parameters. In fact, changing almost any of the parameters in the sloppy models we've studied will rapidly change the behavior. How is this possible? Didn't we just say that the parameters could vary over huge ranges?

 

At left you can see the parameters which fit experiment for a model of circadian rhythms. (This is a two-dimensional view of a 36-dimensional parameter space.) Notice that the good parameters at each temperature form a thin needle-like region. For the blue region at 25 degrees Centigrade, changing one parameter (moving horizontally or vertically alone) will quickly leave the needle, causing big changes in behavior. But the error estimates on each parameter (the total range of variation in the horizontal and vertical direction) are huge. In sloppy models, most directions in parameter space are sloppy (poorly constrained by the behavior), but there are a few stiff directions in parameter space (tightly constrained). These stiff directions allow useful predictions to be made, and allow one to change the model behavior by moving parameters.

To learn more about features of sloppy models and where they arise, see What are Sloppy Models?

References

More on sloppiness:

Research Area: 
Sloppy Models