Why is science possible?

Our group has discovered a striking similarity between theories of physics and more general models used to study complex systems such as in systems biology, economics, ecology, climate science, etc.

Over the past decade, we have been studying a wonderful commonality in these more general systems. Their collective behavior depends mostly on a few "stiff' combinations of rules; most other combinations are sloppy, with little or no influence on system behavior.

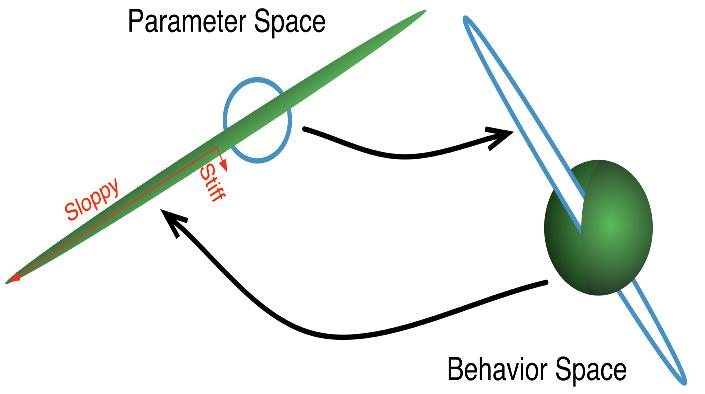
Sloppy models are multiparameter models, whose behavior depends only on a few stiff combinations of parameters, with many sloppy parameter directions largely unimportant for model predictions. We've found them ubiquitous in systems biology and in other fields of science where models are fit to data.

We describe the possible system behaviors as points in a 'behavior' space, and we find that they form a hyper-ribbon, long along stiff combinations and very thin (reflecting unchanging behavior) when sloppy combinations are changed (fig below right). Theories of cell behavior (and presumably ecosystems and economics) don't need to reflect all the details; a useful theory needs only to capture the collective, 'stiff' behaviors.

Hyperribbon structure in behavior space, for the diffusion equation after three evolution steps. Note that it is longer than it is wide, and it is very thin -- like a ribbon.

Theoretical physics, in fact, works precisely for this same reason. We don't need to know the shapes and sizes of individual molecules to make a theory of sound waves; only the overall density and compressibility (weight and squeezability) matter. High energy physicists don't need to solve string theory to predict the Higgs boson, or to describe quarks.

Indeed, theoretical physics is like a tree (figures below). Our high-energy colleagues study the limbs of the tree, searching for more unified theories closer to the trunk. We in condensed matter physics build outward, searching for 'emergent' branches and leaves -- effective theories describing sound, semiconductors, and superfluids.

Does physics share the 'sloppy model' behavior we found in other sciences? We generalized our information geometry methods and applied them to two standard physics models -- diffusion and the Ising model (figure at left). The diffusion equation describes how perfume goes from her skin to your nose (if the air is still). It is usually derived as a continuum limit, using methods similar to those we use for describing many other phases and phenomena in condensed matter physics -- sound, magnets, and superconductors. The Ising model of magnetism, which becomes fractal, is usually analyzed using renormalization group similar to methods used in high-energy physics. Our method, different from continuum limits and renormalization group methods, examines different combinations of the microscopic rules, finding the stiff and sloppy directions. The figure at left shows that the diffusion equation and the Ising model share the same spread of stiff and sloppy combinations as do systems drawn from other branches of science. Moreover, the stiff directions directly correspond to the important combinations that the traditional continuum limit and renormalization-group methods identified as the collective, emergent control parameters.

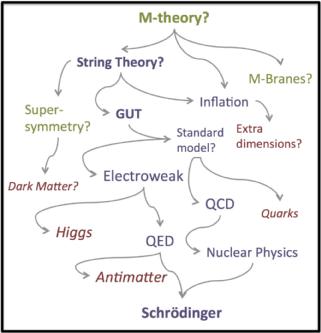
High Energy Physics. Theories in high-energy physics form a nested hierarchy. Each theory is derived from a more fundamental, unified theory, describing behavior at higher energy scales (demanding bigger particle accellerators). The unified theory explains key parameters in the derived theory: quantum chromodynamics and the electroweak theory tell you the masses of the nuclei and electron.

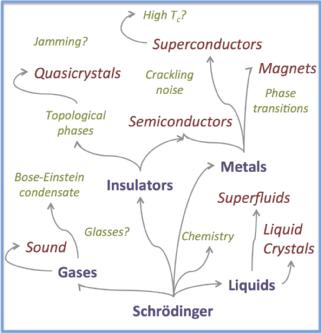
Condensed-matter physics. Theories in condensed-matter physics form a nested hierarchy. Each theory emerges from a more microscopic and complicated theory 'below' it, providing a simpler and more beautiful description. The emergent theory compresses the microscopic details into a few governing parameters that efficiently describe the behavior at longer distances, longer times, and lower temperatures.

So, physics, systems biology, and presumably much of the rest of science all rely on a kind of information compression about the system rules. The collective system behavior in each case relies on only a few 'stiff' combinations of parameters from the many variables in the full microscopic description. In physics, we have systematic methods for extracting these emergent, collective theories from the microscopic complexity. In other fields, we don't have such tools -- but the theories show the same kind of independence from the microscopic details.

If one needed to extract every detail of the true underlying theory to make a useful theory, science would be impossible. Sloppiness makes science possible.

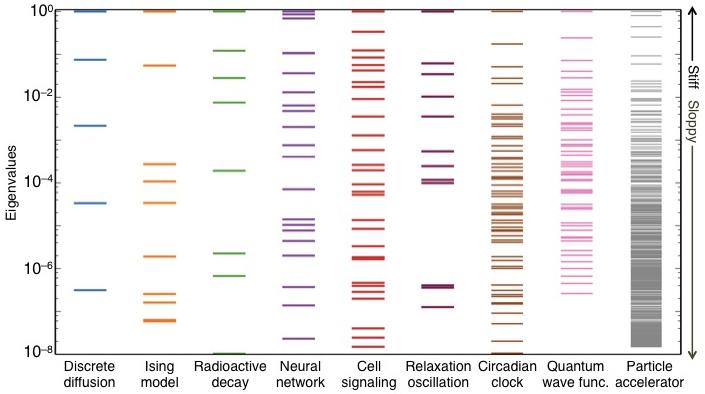
Sloppy Eigenvalues. We use our 'sloppy model' analysis tools to study the hierarchy of models in theoretical physics. We find exactly the same parameter compression behavior in physics as we found in systems biology and other fields of science. Only a few 'stiff' combinations of parameters determine the system behavior.

References and Videos

• Parameter Space Compression Underlies Emergent Theories and Predictive Models, Benjamin B. Machta, Ricky Chachra, Mark K. Transtrum, James P. Sethna, Science 342, 604-607 (2013). See also Physicists unify the structure of scientific theories in the Cornell Chronicle (Anne Ju).
• Jesse Silverberg's Huffington Post blog and Kathryn McGill's vlog Soft Matters with Jim Sethna from The Physics Factor.
• (Unedited) Interview of Sethna by Steven Reiner, Stony Brook School of Journalism, from a workshop by the Alan Alda Center for Communicating Science sponsored by the Kavli Institute at Cornell, May 2013. Mobile version.
• News article on our paper showing physics is sloppy too
• The Secret Simplicity of Science, an AI video describing our work by From Coin Flips to Culture Wars by chargeDeficit.
• Other papers on sloppy models

More on sloppiness:

• Sloppy Models
  • A sloppy systems biology model
  • What is Sloppiness?
  • What are Sloppy Models?
  • Fitting Exponentials: Prediction without parameters
  • Fitting Polynomials: Where is sloppiness from?
  • Why sloppiness? The Sloppy Universality Class
  • Differential Geometry and Sloppy Models (Transtrum)
    • The Model Manifold and Hyperribbons (Transtrum)
    • Sloppy Curvature (Transtrum)
  • Why is science possible? Sloppy models in Physics.
    • Jessie Silverberg's Huffington Post article and Katheryn McGill's vlog Interview from The Physics Factor.
    • Unedited workshop interview by Steven Reiner, Stony Brook School of Journalism; Mobile version.
• Sloppy model applications
  • Do parameters matter? Fits versus measurements.
  • Experimental design in sloppy systems
  • Robustness and sloppiness
    • Parameter robustness and sloppiness
    • Environmental robustness and sloppiness: Circadian rhythms
    • Evolvability, robustness, and sloppiness
  • Estimating systematic errors for interatomic potentials and for density functional theory.
  • Learning digits with InPCA
  • Visualizing the learning trajectories of deep neural networks using InPCA

James P. Sethna, sethna@lassp.cornell.edu; This work supported by the Division of Materials Research of the U.S. National Science Foundation, through grant DMR-1005479.

Statistical Mechanics: Entropy, Order Parameters, and Complexity, now available at Oxford University Press (USA, Europe).