Evolvability, Robustness, and Sloppiness

The Black Death in the 14th century wiped out 2/3 of the population in Europe, presumably leaving mostly people who had natural resistance to the disease. Paleontologists believe the dinosaurs became extinct due to a big environmental change (perhaps triggered by a cometary impact), while mammals survived. The survival of a species is determined not only by how fit it is, but also by how evolvable it is - its ability to adapt to changes in its environment. The species evolvability is a product both of the evolvability of its members and of the genetic diversity within the population.

One would think that evolvability of an individual comes only at the cost of robustness. Robustness is a virtue for engineering systems; having performance that is not disturbed by manufacturing errors (parameter robustness) or changes in circumstance (environmental robustness) makes for higher profits. A cell or mammal whose internal control and signaling systems are robust to mutations and other changes to its internal rates will survive and reproduce more successfully on the short term. But on the other hand, it will be less able to adapt to long-term changes in environment, and hence be less evolvable. Wagner, in studying robustness and evolvabiity in RNA folding (reference below), found that more robust individuals (genotypes) were in fact less evolvable, but also found that more robust species (phenotypes) could have more genetic diversity. The ability of some members of the population to adapt and survive - the species evolvability - was much higher than the typical evolvability of an individual, and higher robustness could lead to a net higher species evolvability.

But what does this all have to do with sloppiness? Sloppiness is a property of systems with many parameters - like the chemical reactions in a cell that help it respond to external signals. The behavior of a sloppy model does depend on its parameters, but only on a few stiff combinations of parameters - so the system behavior can change only in a few ways, one for each stiff direction. Can we measure evolvability and robustness in sloppy systems, and quantify their relationships? Looking at the geometry of sloppy systems may give us a clue.

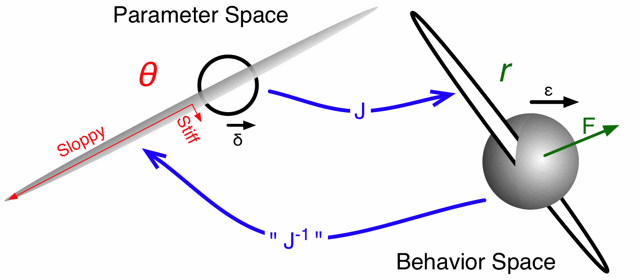
How microscopic rates affect measurable behavior. A small region (sphere) of "fit" behaviors corresponds to a needle-like region of parameters (since sloppy directions in parameter space don't matter to the behavior). On the other hand, a small region (circle) in parameter space (say, from mutations) leads to a thin, stretched range of behaviors (with only the stiff directions in parameter space leading to changes in behavior). Analyzing a sloppy system, we can calculate the fraction of mutations in parameter space that preserves the behavior (robustness), and the probability that an environmental change (force F on the behavior) can be accomodated by a mutation (evolvability).

Looking at the figure, we see that a small circle of mutations leads to a long, thin ellipse of behavior changes. The individual will be evolvable to an environmental pressure F insofar as it lies along a long axis of the ellipse. We can measure robustness by considering the converse problem. The region of parameter space with unchanged behavior is long and needle-like; the volume of this needle inside the circle of possible mutations is the mutational robustness.

Using our model for cell response to hormones and some linear algebra (see paper below), we can answer some of the questions posed about evolvability, robustness, and sloppy models.

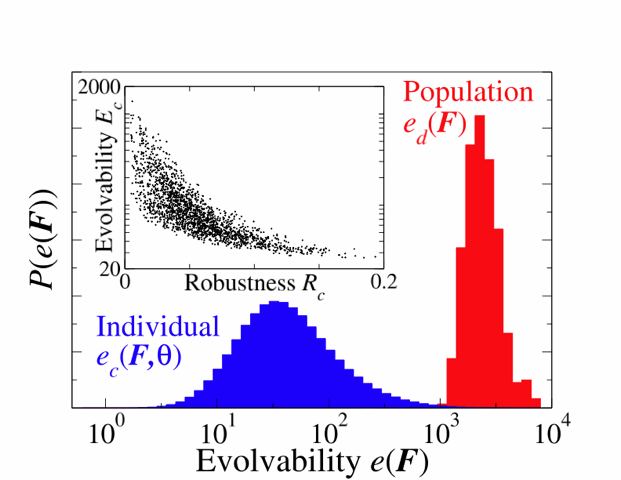
Evolvability and robustness for our signal transduction model. Shown are the relative distributions of how evolvable individuals (blue) and populations (red) are to environmental pressures F. The population is much more able to adaptively mutate than are the typical individuals; the sloppy directions allow for lots of genetic variation without sacrificing the currently adaptive behavior. Inset: For individuals, more robustness to mutations leads to lower net evolutionary adaptability; if robust, mutations don't change the behavior.

• Are more robust individuals less evolvable? Yes. We define the net evolvability of an individual E_c as the average evolvability under all possible forces F. The inset in the figure above shows that the larger the robustness, the lower the evolvability, at least for our model.
• Is the evolvability of the population significantly higher than the individual? Yes. We define the population evolvability e_d(F) to be the maximum of evolvability to a given force in the entire population. The main figure above shows two histograms: one of the various individual evolvabilities (for different forces and different individuals in our ensemble), and the population evolvability. The population evolvability is several hundred times higher. Sloppy directions allow for genetic diversity, which allows a few individuals to be poised to adapt to changing circumstances.
• Are robust species more evolvable? We don't know (yet), since we only looked at one population.

References

"Sloppiness, robustness, and evolvability in systems biology", Bryan C. Daniels, Yan-Jiun Chen, James P. Sethna, Ryan N. Gutenkunst, and Christopher R. Myers, Curr Opin Biotechnol 19, 389-395 (2008), doi:10.1016/j.copbio.2008.06.008, pdf, and supplemental material
• Other papers on sloppy models

More on sloppiness:

• Sloppy Models
  • A sloppy systems biology model
  • What is Sloppiness?
  • What are Sloppy Models?
  • Fitting Exponentials: Prediction without parameters
  • Fitting Polynomials: Where is sloppiness from?
  • Why sloppiness? The Sloppy Universality Class
  • Differential Geometry and Sloppy Models (Transtrum)
    • The Model Manifold and Hyperribbons (Transtrum)
    • Sloppy Curvature (Transtrum)
  • Why is science possible? Sloppy models in Physics.
    • Jessie Silverberg's Huffington Post article and Katheryn McGill's vlog Interview from The Physics Factor.
    • Unedited workshop interview by Steven Reiner, Stony Brook School of Journalism; Mobile version.
• Sloppy model applications
  • Do parameters matter? Fits versus measurements.
  • Experimental design in sloppy systems
  • Robustness and sloppiness
    • Parameter robustness and sloppiness
    • Environmental robustness and sloppiness: Circadian rhythms
    • Evolvability, robustness, and sloppiness
  • Estimating systematic errors for interatomic potentials and for density functional theory.
  • Learning digits with InPCA

By Yan-Jiun Chen (chen.yanjiun@gmail.com) and James P. Sethna (sethna@lassp.cornell.edu). This work supported by the Division of Materials Research of the U.S. National Science Foundation, through grant DMR-070167.

Statistical Mechanics: Entropy, Order Parameters, and Complexity, now available at Oxford University Press (USA, Europe).