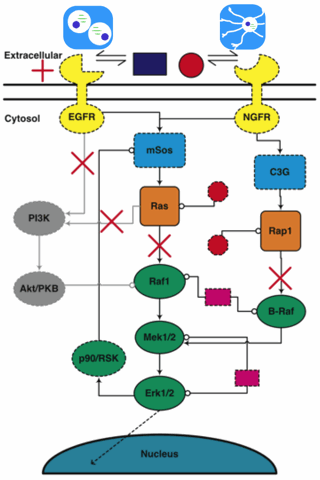
Some years back, Colin Hill (then a Physics graduate student of mine, now CEO of Gene Network Sciences) got interested in biology. He dragged me out to talk with Rick Cerione (then in Molecular Medicine at the Vet college) and his student Guillermo Calero about how proteins interact to transmit signals inside cells (and how, when they mutate, cells can become cancerous). Another student, Kevin Brown, soon got involved, and we stumbled onto the existence of sloppy models...

The multiparameter model

Interacting proteins. Biologists usually draw pictures with lines connecting proteins. Here there are two hormones (EGF = Epidermal Growth Factor, blue rectangle, and NGF = Neuronal Growth Factor, red circle) outside the cell membrane (double black lines), that attach to their corresponding receptors. The receptors then activate Sos and either PI3K or C3G (various proteins), which activate more proteins, ..., which eventually activates Erk, which then carries the message into the nucleus. How the activated Erk varies in time determines whether the cell proliferates (doubles, under EGF) or differentiates (turns part-way into a neuron, under NGF) as shown in blue.

The differential equations, drawn too small to read, corresponding to the model at left. The blowup shows one of the nonlinear differential equations, which happens to have six parameters determining how fast reactions run and saturate. Computers are fast, and graduate students are tough - it's not a challenge to type in and run these equations. But Cerione explained that none of the parameters are known to better than a factor of between two and ten, and that it was so boring to measure them that he couldn't pay anyone to do so. The model has 48 total parameters!

I figured that we'd never be able to extract 48 parameters from fitting the data. Rick Cerione, though, expected that we'd be able to make predictions anyway. Always before, he could make predictions in his head! With a computer we ought to be able to include a few more feedback loops?

Parameters fluctuate over enormous range

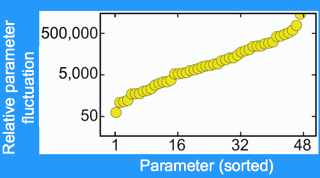Huge parameter variations. The factor by which each parameter varies, with parameters sorted in increasing order. Every parameter varies by more than a factor of fifty. Will predictions be possible?

We could fit to the data and make predictions, but with 48 free parameters could we trust our answers? To see if an answer was trustworthy, we did statistical mechanics in model space. (Doing a Monte Carlo in parameter space, it turns out, is called stochastic Bayesian analysis.) As I had suspected, the parameters varied over huge ranges. In fact, every parameter varied by over a factor of fifty, and many varied over factors of many thousands. Remember - all of these parameter sets still fit the existing experimental data.

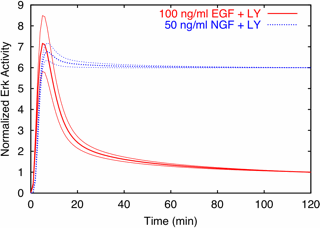
Predictions are possible without parameters!

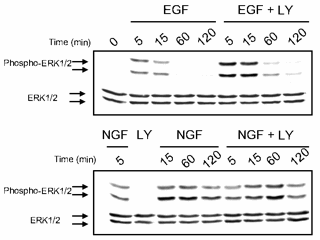Predictions are possible, even with huge uncertainties in all parameters. Predicted time evolution of activated Erk after stimulation with growth hormones EGF and NGF, after PI3K is inactivated by the use of the drug LY. Notice that the uncertainties are only a few percent, even though the uncertainty in every parameter individually is larger than a factor of fifty!	Prediction verified by experiment. The key part of this Western blot are the blots in the upper right (in the row Phospho-ERK1/2, column EGF+LY). The blots are dark (lots of Erk activity) at 5 and 10 minutes, and then grow light, just as for the prediction, red curve at left. The blue curve at left corresponds to the column NGF+LY, which indeed stay dark (active) all the way to 120 minutes.

What's weird, however, is not that we got the prediction correct - it is that we were able to predict anything at all. To understand how this is possible, see What is Sloppiness?

References

• "The Statistical Mechanics of Complex Signaling Networks: Nerve Growth Factor Signaling", Kevin S. Brown, Colin C. Hill, Guillermo A. Calero, Christopher R. Myers, Kelvin H. Lee, James P. Sethna, and Richard A. Cerione, Physical Biology 1, 184-195 (2004) . (pdf,, and supplemental material.)
• "Statistical Mechanics Approaches to Models with Many Poorly Known Parameters", Kevin S. Brown and James P. Sethna, Phys. Rev. E 68, 021904 (2003). (pdf.)
• Other papers on sloppy models

More on sloppiness:

• Sloppy Models
  • A sloppy systems biology model
  • What is Sloppiness?
  • What are Sloppy Models?
  • Fitting Exponentials: Prediction without parameters
  • Fitting Polynomials: Where is sloppiness from?
  • Why sloppiness? The Sloppy Universality Class
  • Differential Geometry and Sloppy Models (Transtrum)
    • The Model Manifold and Hyperribbons (Transtrum)
    • Sloppy Curvature (Transtrum)
    • Model Manifold Comparisons of Algorithms (Kloumann)
  • Why is science possible? Sloppy models in Physics.
    • Jessie Silverberg's Huffington Post article and Katheryn McGill's vlog Interview from The Physics Factor.
    • Unedited workshop interview by Steven Reiner, Stony Brook School of Journalism; Mobile version.
• Sloppy model applications
  • Do parameters matter? Fits versus measurements.
  • Experimental design in sloppy systems
  • Robustness and sloppiness
    • Parameter robustness and sloppiness
    • Environmental robustness and sloppiness: Circadian rhythms
    • Evolvability, robustness, and sloppiness
  • Estimating systematic errors for interatomic potentials and for density functional theory.